- Startseite
- Allgemeine Informationen zur Lehrveranstaltung
- Einfaches Python Setup und Wichtige Informationen
- 0. Python Einführung und Checkup
- 1. Einführung und einfache Algorithmen
- 2. Differenzieren und Integrieren
- 3. Vektoren, Matrizen und Vektorisierung in Python
- 4. Datenanalyse bzw. Datenauswertung
- 5. Grundlagen der Optimierung und Gradient Descent
- 6. Stochastische Optimierung und Genetische Algorithmen
- 7. Monte-Carlo-Methoden – Simulation und Integration
- 8. Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk
- 9. Unsupervised Machine Learning: Clustering von Daten
- 10. Supervised Machine Learning: Grundlagen
- 11. Einführung in künstliche neuronale Netzwerke
Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.
9 Unsupervised Machine Learning: Clustering von Daten¶
In dieser Einheit Beschäftigen wir uns mit einer interessanten Methode, um Daten zu “ordnen”, dem Clustering. Damit tauchen wir ein Stück in das Gebiet des Machine Learnings ein, genauer gesagt, gehört dieser Ansatz zum sogenannten “unsupervised learning”. Das bedeutet, dass man über den Datensatz nicht allzuviel wissen muss, um ihn in Kategorien (bzw. Cluster) einteilen zu können oder ihn besser verstehen zu lernen.
Allerdings ist auch nicht von vornherein klar, dass es eine Struktur in den Daten gibt, die eine signifikante Bedeutung hat. Damit Sie das besser verstehen, sehen wir uns am besten gleich ein Beispiel an. Ich habe diemal wieder ein Stück aus einem Dataset von kaggle.com vorbereitet. Genauer gesagt, von der folgenden Quelle: https://www.kaggle.com/datasets/grisme/hourly-snapshots-of-lightning-network Nehmen Sie eine beliebige CSV Datei aus dem Unterordner “nodes” des Datensatzes (wir verwenden hier _2019_12_11_16_0537.csv) und benennen Sie diese entsprechend auf ‘lightning_strokes.csv’ um. Im Moodle finden Sie dieses Beispiel fertig zum Download, sodass Sie sich nicht das gesamte Dataset herunterladen müssen.
Hier aber zunächst noch die Imports für heute:
%matplotlib inline
import matplotlib.pyplot as plt # für plotting, wie gewohnt
import numpy as np # für numerische Aktionen mit Arrays, wie gewohnt
import pandas as pd # für das Einlesen der Daten
import os # Funktionen zum OS
from sklearn.cluster import AgglomerativeClustering # für Clusteringmethode 1
from sklearn.cluster import DBSCAN # für Clusteringmethode 2
from sklearn.cluster import KMeans # für Clusteringmethode 3
# Lade Daten aus einer der Dateien
raw_data = pd.read_csv(os.path.join('data', 'lightning_strokes.csv'), delimiter=',')
# Nimm nur jene Zeilen, wo es geografische Koordinaten gibt. Das bedeutet
# in diesem Fall Koordinaten, die ungleich 0 sind
raw_data_notempty = raw_data[raw_data["geo"] != "{'latitude': 0, 'longitude': 0}"]
# Aus diesen Daten, extrahiere die Spalte "geo"
raw_data_coordinates = raw_data_notempty["geo"]
# Wie sieht das aus?
raw_data_coordinates.head(20)
# das ist jetzt im Prinzip eine Reihe von Dictionaries.
# Wir machen daraus als nächstes ein NumPy-Array
0 {'latitude': 51.2993, 'longitude': 9.491}
1 {'latitude': 39.9653, 'longitude': -83.0235}
3 {'latitude': 58.4167, 'longitude': 15.6167}
6 {'latitude': 52.0947, 'longitude': 5.0947}
7 {'latitude': 37.751, 'longitude': -97.822}
11 {'latitude': 38.6582, 'longitude': -77.2497}
14 {'latitude': 44.4914, 'longitude': 26.0602}
15 {'latitude': 46.2022, 'longitude': 6.1457}
16 {'latitude': 32.7824, 'longitude': -97.3003}
18 {'latitude': 37.4056, 'longitude': -122.0775}
20 {'latitude': 43.7801, 'longitude': -79.3479}
21 {'latitude': 50.2279, 'longitude': 9.3478}
25 {'latitude': 56, 'longitude': 24}
26 {'latitude': 32.2827, 'longitude': 34.9105}
29 {'latitude': 40.4172, 'longitude': -3.684}
31 {'latitude': 40.7185, 'longitude': -74.0025}
34 {'latitude': 52.3824, 'longitude': 4.8995}
38 {'latitude': 39.0481, 'longitude': -77.4728}
40 {'latitude': 41.9399, 'longitude': -87.6528}
42 {'latitude': 56.6616, 'longitude': 16.3616}
Name: geo, dtype: object# das ist eine kleine Fingerübung in String Manipulation und impliziten Listen
data_array = np.array([ [(a_string.strip("{}").split())[3].strip(","),
(a_string.strip("{}").split())[1].strip(",")]
for a_string in raw_data_coordinates.to_numpy()
]).astype(float)
# somit haben wir ein Array von floats
data_array
array([[ 9.491 , 51.2993],
[-83.0235, 39.9653],
[ 15.6167, 58.4167],
...,
[ -9.2545, 38.7566],
[-73.9644, 40.679 ],
[135.52 , 34.6864]])# sehen wir uns diese Daten mal an. Werden die sich fürs Clustern eignen?
fig = plt.figure(figsize=(15,10))
# setze einen geeigneten Wert für das Bild-Seitenverhältnis
ax = plt.gca()
ax.set_aspect(.75)
# Ein Scatterplot, wie wir ihn schon gewöhnt sind
plt.scatter(*np.transpose(data_array))
# Achsenbeschriftungen
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.show()
9.1 Was ist bzw. macht ein Clustering-Algorithmus eigentlich?¶
Bevor wir uns jetzt ans Clustering machen, möchte ich noch eine Runde erklären, was das eigentlich kann und tun soll. Dadurch wird sich auch die Frage beantworten, die ich gerade vorher im Kommentar gestellt habe, nämlich: Werden diese Daten sich fürs Clustern eignen?
Ein Clustering-Algorithmus teilt einen Datensatz in Gruppen ein. Das passiert auf der Basis der Eigenschaften der Daten untereinander, z.B. wie “benachbart” sie sind (was auch immer das dann im Detail heißen mag). Wenn wir Daten haben, die 2-dimensionalen Koordinaten entsprechen (so wie in unserem Beispiel), dann ist die Sache recht anschaulich. Das werden wir hier also auch so verwenden und uns ansehen. Das muss aber nicht so sein. Sie können Daten verwenden, für die eine Ähnlichkeit recht umständlich definiert ist, oder sogar erst definiert werden muss.
Für das Clustering selbst (also die Gruppeneinteilung von Daten) gibt es verschiedene Algorithmen, die verschiedene Parameter für das Gruppieren nutzen. Lassen Sie uns also zunächst einmal diese Parameter kurz durchsehen:
- Die Anzahl der gewünschten/vermuteten Cluster: Manche Algorithmen, wie z.B. K-Means (siehe weiter unten) verlangen die Festlegung auf eine bestimmte Anzahl von Clustern von vornherein. Das bedeutet, man legt z.B. 3 Cluster fest, clustert dann die Daten so und sieht (bzw. kann berechnen), wie gut diese Wahl gepasst hat.
- Ein bestimmter Abstand, den die Elemente maximal haben dürfen, um zum gleichen Cluster zu gehören, oder etwas Derartiges. Das kann ein einzelner Abstand oder ein gemittelter sein, je nachdem. So etwas setzt auch voraus, dass man zumindest irgendeine Ahnung von der ungefähren Dimension so eines Clusters hat.
- Die Art der Daten und zwar entweder absolute Koordinaten oder Distanzen: Manche Algorithmen brauchen gar keine absoluten Distanzen, um ein Clustering berechnen zu können, sondern nur die Distanzen zwischen allen Elementen der Daten. Das Agglomerative Clustering, das wir uns gleich ansehen werden, ist so ein Algorithmus. Diese Variante (nur Distanzen) kann ziemlich praktisch sein, vor allem dann, wenn man die Abstandsmessung, die man zur Verfügung hat, nicht so einfach in koordinaten umsetzen kann. Denken Sie z.B. an eine Sequenzähnlichkeit von Buchstabenketten oder DNA.
- Die Art, wie die Distanzen berechnet werden: Z.B. kann man immer die kleinste Distanz eines Elements zu einem bereits bestehenden Cluster nehmen, oder die gemittelten Distanzen des Elements zu allen Elementen eines bestehenden Clusters, oder dergleichen mehr.
Insgesamt läuft es darauf hinaus, dass man, je nach Algorithmus, die eine oder andere Vorgabe machen muss, damit der Algorithmus arbeiten kann. Andere Parameter kommen jeweils dann als Resultat heraus oder kommen nicht vor.
Wir sehen uns jetzt drei verschiedene Algorithmen nacheinander an, die etwas verschieden funktionieren. Mit jedem davon könnten wir viel mehr Zeit verbringen, die wir allerdings nicht haben. Daher erkläre ich jeweils nur kurz das Grundprinzip, zeige Ihnen den grundlegenden Aufruf aus der Package Scikit-Learn, und wir vergleichen den Output für jeweils einen zentralen Parameter.
Aber keine Sorge: In der Übungsaufgabe sind Sie dann wieder zum Experimentieren mit dem Clustering dieser Daten aufgerufen.
9.2 Der Algorithmus Agglomerative Clustering, kurz und einfach erklärt, mit Beispiel¶
Agglomeratives Clustering wird auch als “hierarchisches” Clustering bezeichnet. Warum, das ergibt sich aus der Funktionsweise. Die Schritte bei dieser Art des Clusterings ist wie folgt:
- Die Distanzen zwischen allen Datenpunkten werden berechnet (oder sie sind anstelle von absoluten Koordinaten bereits gegeben, siehe oben)
- Die beiden Datenpunkte mit der kürzesten Distanz werden zu einem Cluster kombiniert.
- Dieser Cluster wird entweder durch alle seine Mitglieder repräsentiert und deren Koordinaten bleiben für Vergleiche verfügbar, oder er bekommt eine zentrale Koordinate zugewiesen
- Für den neuen Cluster werden alle Distanzen zu den anderen Punkte im Datensatz berechnet
- Die beiden Datenpunkte (inklusive des neuen Clusters) mit der kürzesten Distanz werden wieder zu einem neuen Cluster kombiniert.
- Das kann so vor sich gehen, dass entweder der erste Cluster wächst oder ein separater neuer Cluster aus zwei einzelnen Datenpunkten entsteht und der erste Cluster unverändert bleibt.
- Dieser Vorgang wiederholt sich so oft, bis alle Punkte Clustern zugeordnet sind.
- Das führt letztendlich dazu, dass am Ende alle Daten in einem riesigen Cluster landen, dass allerdings gleichzeitig die Hierarchie innerhalb des Clusters über einen Baumgraphen klar ist
- Wenn man tatsächlich mehrere Cluster erhalten möchte, dann muss man mit dem Kombinieren aufhören, bevor alles in einem Cluster landet. Das geht entweder über eine Maximale Distanz, bei der aufgehört wird, oder über eine bestimmte Anzahl von Clustern, die man haben möchte, und bei der dann aufgehört wird.
Insgesamt ist diese Methode sehr mächtig. Wir sehen uns jetzt einmal konkret an, was Agglomeratives Clustering aus unseren Beispieldaten macht. Der Grundaufruf der Klassen aus Scikit-Learn ist immer der gleiche: Wir generieren eine Instanz der Klasse soundso und davon holen wir uns dann die sogenannten “Labels”, d.h. die Zahlen, die für jedes Element im Datensatz die Clusterzugehörigkeit anzeigen. So sieht das aus:
# Erzeuge eine Instanz der Clustering-Klasse, mit 4 Clustern voreingestellt
# und fitte damit die Daten in unserem Daten-Array
first_clustering = AgglomerativeClustering(n_clusters=4, compute_full_tree=False).fit(data_array)
# So bekommt man die Indizes für die Cluster-Zugehörigkeit
# die kann man perfekt zum Einfärben der Punkte in einem Scatterplot nutzen
first_clustering.labels_
array([2, 0, 2, ..., 2, 0, 1])
# Grafische Darstellung
fig = plt.figure(figsize=(15,10))
# setze einen geeigneten Wert für das Bild-Seitenverhältnis
ax = plt.gca()
ax.set_aspect(.75)
# Scatterplot mit den Daten, so wie oben, nur mit den Farben nach Clusterlabels
the_plot = plt.scatter(*np.transpose(data_array), c=first_clustering.labels_, cmap='tab20b')
# Zeichne zusätzlich noch einen Balken mit den Werten zu den Farben
plt.colorbar(the_plot, orientation="vertical", shrink=0.3)
# Achsenbeschriftungen
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.show()
So stellt sich der Algorithmus also die Daten in 4 Clustern vor. Das kann man jetzt gut finden oder auch nicht, aber damit geben wir uns natürlich nicht zufrieden. Daher lassen wir einen Loop über verschiedene Anzahlen von Clustern laufen und sehen uns die Ergebnisse nebeneinander an. Dabei zeigt ein Colorbar an der Seite jeweils an, wie die Farben zu den Nummern der Cluster gehören.
# setzen wir die maximale Cluster-Anzahl auf 15
max_n = 15
# Starte die Grafik
fig = plt.figure(figsize=(15,70))
# Definiere die Liste für die Cluster-Anzahlen
cluster_range = range(2, max_n+1)
# Loop über die Anzahl der Cluster
for an_n in cluster_range:
# Erzeugen des Clusterings. Die Clusteranzahl sollte sinnvollerweise mindestens
# bei 2 beginnen
first_clustering = AgglomerativeClustering(n_clusters=an_n, compute_full_tree=False).fit(data_array)
# Erzeuge einen Subplot, 10x1 Plots insgesamt, dieser an der Stelle N+1
ax = plt.subplot(len(cluster_range),1,an_n-1)
# setze einen geeigneten Wert für das Bild-Seitenverhältnis
ax.set_aspect(.75)
# Und der Scatterplot mit den eingefärbten Punkten für dieses Clustering
the_plot = ax.scatter(*np.transpose(data_array), c=first_clustering.labels_, cmap='tab20b')
# Zeichne zusätzlich noch einen Balken mit den Werten zu den Farben
plt.colorbar(the_plot, orientation="vertical", shrink=0.7)
# Setze Achsenbeschriftungen und eine Plotüberschrift
ax.set_xlabel("Longitude")
ax.set_ylabel("Latitude")
ax.set_title("Number of Clusters:"+str(an_n))
# Und den Plot anzeigen
plt.show()
9.3 Der Algorithmus DBSCAN, kurz und einfach erklärt, mit Beispiel¶
Als nächste Möglichkeit sehen wir uns einen Algorithmus an, der als DBSCAN bekannt ist. Diese Abkürzung steht für Density-Based Spatial Clustering of Applications with Noise, und das funktioniert wie folgt:
- Der Algorithmus durchsucht die Datenpunkte der Reihe nach, und klärt für jeden Datenpunkt, ob er ein core-sample ist
- Ein core-sample ist dadurch gekennzeichnet, dass es von einer bestimmten Anzahl anderer Samples höchstens einen bestimmten Abstand hat.
- Durch dieses Konzept der mindestens soundsoviele Punkte mit höchstens diesem Abstand voneinander wird eine Dichte beschrieben (daher density-based)
- Ein Cluster besteht dann in diesem Fall aus einer zusammenhängenden Menge von core-samples und allen Punkten, die von einem dieser core-samples höchstens den vorbestimmten Abstand haben (die selber aber keine core-samples sind, weil sie am Rand eines Clusters liegen, bzw. dort, wo er “weniger dicht” wird).
- Alle Punkte, die nicht innerhalb des vorgegebenen Abstands zu einem core-sample liegen, werden als Ausreißer bzw. Noise (Rauschen) gewertet und bekommen einen extra Label zugewiesen
- Kritische Parameter hier sind also:
- Der Abstand, der die Dichte bestimmt, und
- Die minimale Anzahl von Punkten, die es braucht, um core-samples zu finden
Schauen wir uns zunächst einmal von einem solchen Clustering den Output an:
second_clustering = DBSCAN(eps=15).fit(data_array)
# Damit wir nicht Listen dursehen müssen, plotten wir ein Histogramm
fig = plt.figure()
# Hier ist es, die möglichen Werte beginnen bei "-1", das steht für "outlier" oder "noise"
# und die anderen sind Cluster-Indizes
plt.hist(second_clustering.labels_, bins=[-1,0,1,2,3,4,5,6,7,8])
# setze y-Skalierung auf logarithmisch, zur besseren Sichtbarkeit
plt.yscale("log")
# Achsenbeschriftungen
plt.xlabel("Cluster-Index")
plt.ylabel("Count/Cluster-Size")
plt.show()
Jetzt können wir natürlich auch hier einen Loop laufen lassen, der uns mehrere Darstellungen unseres Datensatzes mit verschiedenen Parametern zeigt. Am wichtigsten ist hier der voreingestellte Abstand, weshalb wir diesen über Werte in einer Liste variieren werden.
In den Figuren, die im Folgenden erzeugt werden, sehen Sie an der Seite wieder das Colorbar. Dort können Sie auch anhand der Skala sehen, wie viele Cluster jeweils erzeugt wurden.
# Erzeuge die Figur
fig = plt.figure(figsize=(15,45))
# Loop über mehrere Werte des Abstands. Da wir auch den Index dazu brauchen,
# ist hier ein enumerate eingesetzt
for counter, an_n in enumerate([1, 2, 5, 10, 15, 20, 30, 50]):
# Erzeuge das Clustering mit DBSCAN und dem entsprechenden Abstand
second_clustering = DBSCAN(eps=an_n).fit(data_array)
# Erzeuge einen Subplot, hier haben wir 8
# Werte im 8x1 Anordnung, numeriert durch den Zähler
ax = plt.subplot(8,1,counter+1)
# setze einen geeigneten Wert für das Bild-Seitenverhältnis
ax.set_aspect(.75)
# Und der Scatterplot mit den eingefärbten Punkten für dieses Clustering
the_plot = ax.scatter(*np.transpose(data_array), c=second_clustering.labels_, cmap='tab20b')
# Zeichne zusätzlich noch einen Balken mit den Werten zu den Farben
plt.colorbar(the_plot, orientation="vertical", shrink=0.7)
# setze Achsenbeschriftungen und Titel für die Subplots
ax.set_xlabel("Longitude")
ax.set_ylabel("Latitude")
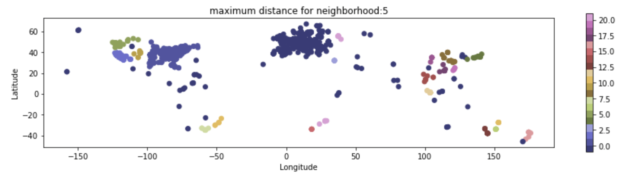
ax.set_title("maximum distance for neighborhood:"+str(an_n))
# Plots anzeigen
plt.show()
Hier sieht man deutlich den Effekt der verschieden eingestellten Abstände. Bei kleinen Werten ergeben sich teils seltsame Muster. Erst bei mittelgroßen Werten erscheint das Clustering auch auf den ersten Blick sinnvoll. Bei zu großen Werten landen wieder alle Punkte in einem einzigen Cluster.
Was man ebenfalls anhand des Colorbars schön sehen kann, sind die jeweils als “Ausreißer” bzw. “Noise” eingestuften, ganz dunkelblauen Punkte.
9.4 Der Algorithmus K-Means, kurz und einfach erklärt, mit Beispiel¶
Als letzten Cluster-Algorithmus sehen wir uns noch einen sehr gebräuchlichen an, nämlich k-means. Dieser Algorithmus setzt ein Prinzip um, das uns vielleicht im Vergleich mit den beiden bisher erklärten noch etwas intuitiver erscheint, was nämlich die Bildung und Definition der Cluster betrifft. Hier sind die Eckpunkte von k-means:
- Die Anzahl $N$ der Cluster muss bei diesem Algorithmus vorgegeben werden und ändert sich auch während der Laufzeit des Algorithmus nicht.
- Der Datensatz wird in $N$ Cluster eingeteilt.
- k-means geht grundsätzlich von Daten auf der Basis von Koordinaten aus. Vorberechnete Differenzen nimmt er nur mit einigen Modifikationen an.
- Für jeden Cluster wird ein sogenanntes “Centroid” berechnet, also das Clusterzentrum. Zu beachten ist, dass das Clusterzentrum im Allgemeinen nicht einem der Datenpunkte im Datensatz entsprechen wird (also quasi ein extra-Punkt ist, der sich im Laufe der Zeit ändert).
- Diese Clusterzentren werden nun so optimiert, dass jeder Datenpunkt zu jenem Cluster gehört, dessen Centroid er am nächsten liegt.
- Das führt zu einer Optimierung der Varianz der Abstände der Datenpunkten zum Centroid in jedem Cluster
- Bei der Optimierung werden im wesentlichen zwei Schritte ausgeführt:
- Zuordnung jedes Datenpunkts zum nächsten Centroid
- Neuberechnung der Centroiden auf der Basis dieser Zuordnung
- Die wiederholte Ausführung dieser beiden Schritte wird bei Konvergenz der Centroiden-Positionen abgebrochen
Sehen wir uns das jetzt einmal in der Praxis an. Der Parameter, den wir hier variieren werden, ist wieder die Anzahl der Cluster.
# Setzen wir die Maximale Zahl der verwendeten Cluster wieder auf 15
max_n = 15
# Erzeuge die Figur
fig = plt.figure(figsize=(15,70))
# Definiere die Liste für die Cluster-Anzahlen
cluster_range = range(2, max_n+1)
# Loop über die Anzahl der Cluster
for an_n in cluster_range:
# Erzeugen des Clusterings. Die Clusteranzahl sollte sinnvollerweise mindestens
# bei 2 beginnen
third_clustering = KMeans(n_clusters=an_n).fit(data_array)
# Erzeuge die Subplots in einem 10x1 Raster
ax = plt.subplot(len(cluster_range),1,an_n-1)
# setze einen geeigneten Wert für das Bild-Seitenverhältnis
ax.set_aspect(.75)
# Und der Scatterplot mit den eingefärbten Punkten für dieses Clustering
the_plot = ax.scatter(*np.transpose(data_array), c=third_clustering.labels_, cmap='tab20b')
# Zeichne zusätzlich noch einen Balken mit den Werten zu den Farben
plt.colorbar(the_plot, orientation="vertical", shrink=0.7)
# Setze Achsenbeschriftungen und Titel für die Subplots
ax.set_xlabel("Longitude")
ax.set_ylabel("Latitude")
ax.set_title("Number of Clusters:"+str(an_n))
# Plots anzeigen
plt.show()
9.5 Übungsaufgabe: Experimentieren mit Clustering-Algorithmen¶
Die heutige Übungsaufgabe lautet: Experimentieren mit Cluster-Algorithmen, und zwar sowohl mit denen, die wir bereits verwendet haben, als auch mit weiteren, wenn Sie möchten. Spielen Sie mit den Parametern und stellen Sie diese so ein, dass Sie die Resultate gut interpretierbar finden würden.
Als weiterer Schritt (optional) bietet sich an, noch weitere Clustering-Algorithmen zu testen. Gehen Sie dazu auf die Überblicksseite für Clustering bei Scikit-Learn und suchen Sie sich etwas aus, von dem Sie glauben, dass es besonders gut zu unserem Datenbeispiel passt.