Hier finden Sie eine Reihe von Fragen, die Sie zum Beispiel aber nicht ausschließlich bei der abschließenden Prüfung zur VU Fortgeschrittene Mathematik und Computergestützte Algorithmen erwarten können. Zur Vorbereitung empfehle ich Ihnen, sich die Fragen durchzulesen und darauf zu achten, ob Sie sie zu Ihrer Zufriedenheit beantworten können. Das soll bedeuten, Sie fühlen sich zuversichtlich, diesen Inhalt auch jemandem erklären zu können, der davon noch nichts gehört hat.
Wenn das nicht der Fall ist, lesen Sie die entsprechende Stelle in diesem Skriptum nach und arbeiten Sie das Thema mit dem Jupyter-Notebook noch einmal in Ruhe durch. Hier sind die Kapitel nochmal als übersichtliche Liste:
- Startseite
- Allgemeine Informationen zur Lehrveranstaltung
- Einfaches Python Setup und Wichtige Informationen
- 0. Python Einführung und Checkup
- 1. Einführung und einfache Algorithmen
- 2. Differenzieren und Integrieren
- 3. Vektoren, Matrizen und Vektorisierung in Python
- 4. Datenanalyse bzw. Datenauswertung
- 5. Grundlagen der Optimierung und Gradient Descent
- 6. Stochastische Optimierung und Genetische Algorithmen
- 7. Monte-Carlo-Methoden – Simulation und Integration
- 8. Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk
- 9. Unsupervised Machine Learning: Clustering von Daten
- 10. Supervised Machine Learning: Grundlagen
- 11. Einführung in künstliche neuronale Netzwerke
Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.
Fragen zu Einführung und einfache Algorithmen
- Geben Sie ein einfaches Beispiel für einen Algorithmus aus dem täglichen Leben!
- Geben Sie ein einfaches Beispiel für einen mathematischen Algorithmus (z.B. mit Zahlen)!
- Erklären Sie anschaulich, was mit der “Komplexität” eines Algorithmus gemeint ist!
- Nennen Sie einige typische charakteristische Merkmale eines Algorithmus!
- Erklären Sie die Bedeutung des Begriffs “iterativ” im Zusammenhang mit Algorithmen!
- Welche beiden Haupttypen von Loops haben wir in Python verwendet und worauf muss man bei deren Verwendung achten?
- Bei unserem Beispiel zur Berechnung der ersten N Primzahlen haben wir zum ersten Mal einen Hauch von “Optimierung” gespürt, als wir versucht haben, die Zeit-Komplexität unseres Beispiel-Algorithmus zur Primzahlenberechnung zu verbessern. Erklären Sie diese Situation und die Zusammenhänge!
- Nennen Sie (zumindest) eine Klasse der Zeitkomplexität!
- Kann ein und dasselbe Problem je nach Lösungsmethode in verschiedene Klassen der Zeitkomplexität gehören? Warum (nicht)?
- Erklären Sie den Begriff der “Skalierung” im Zusammenhang mit der Zeitkomplexität eines Algorithmus!
- Muss eine iterative Lösungsmethode eines Problems grundsätzlich immer konvergieren?
Fragen zu Differenzieren und Integrieren
- Erklären Sie anschaulich den Unterschied zwischen analytischen und numerischen Lösungsmethoden für mathematische Probleme!
- Welche Python Package haben wir für die analytische bzw. symbolische Arbeit an Problemen verwendet?
- Wenn man in SymPy erst einmal Symbole (Variablen) und Funktionen dieser Variablen definiert hat, was kann man dann z.B. damit machen?
- Sie haben mit SymPy eine längere Rechnung symbolisch durchgeführt. Wie bekommen Sie am Ende konkrete Zahlen für bestimmte Werte Ihrer Variablen heraus?
- Beschreiben Sie kurz, wie Sie mit SymPy Gleichungen symbolisch lösen können!
- Beschreiben Sie kurz, wie Sie mit SymPy symbolisch eine Funktion ableiten oder integrieren können!
- Diskutieren Sie anschaulich mögliche Probleme bei der numerischen Differentiation!
- Muss man in Python die Funktionalität für numerisches Differenzieren selbst schreiben?
- Diskutieren Sie anschaulich mögliche Probleme und die Vorteile der numerischen Integration!
- Welches numerische Integrationsverfahren haben wir beispielhaft eingesetzt und mit Hilfe welcher Python-Package?
Fragen zu Vektoren, Matrizen und Vektorisierung in Python
- Welche Python-Package ist bei der Behandlung von Vektoren, Matrizen und höherdimensionalen Arrays zentral?
- Beschreiben Sie kurz die Macht der NumPy-Arrays und wie diese sich von normalen Listen in Python unterscheiden!
- Mit NumPy ist die Erzeugung und Manipulation von Matrizen recht einfach. Zählen Sie ein paar Beispiele für solche Manipulationen auf!
- Eine wesentliche Operation an NumPy-Arrays ist das sogenannte “Slicing”. Worum handelt es sich dabei, und worauf muss man besonders achten?
- Auch die Matrixmultiplikation ist mit NumPy-Arrays kein Problem. Beschreiben Sie ein Beispiel dafür und wie man sie für NumPy-Arrays ganz einfach ausführen kann!
- Als Beispiel für höherdimensionale Arrays haben wir uns mit Bildern und Bildbearbeitung auseinandergesetzt. Wie viele Dimensionen hat das NumPy-Array, das beim Laden einer Fotodatei entsteht und warum?
- Nennen Sie ein Beispiel für eine einfache Bildbearbeitungs-Operation und wie man diese an einem NumPy-Array realisieren würde!
- Beschreiben Sie die generelle Funktionsweise eines Filters und wie man dessen Anwendung auf ein Bild mit NumPy-Hilfe umsetzen kann!
- Was ist, macht und bringt “Vektorisierung” in Python?
- Worauf müssen Sie achten, wenn Sie vektorisierten Python-Code verwenden?
Fragen zu Datenanalyse bzw. Datenauswertung
- Welches gängige Dateiformat haben wir für unsere Daten-Input-Dateien verwendet?
- Was findet man auf kaggle.com?
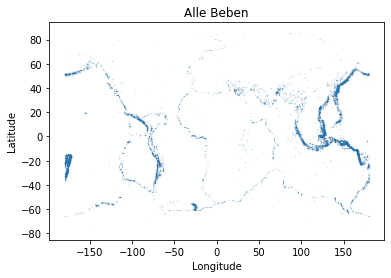
- Als erste Möglichkeit, sich mit Daten vertraut zu machen, bietet sich meist die grafische Darstellung an. Welche Python-Package haben wir dafür verwendet und wie funktioniert sie in etwa?
- Wenn man Daten aus einer Datei einliest, muss man meist etwas Filtern oder Bereinigen. Beschreiben Sie, welche Schritte dabei nötig sein können!
- Nach einer grafischen Darstellung neuer Daten bietet sich eine einfache statistische Auswertung der Daten als nächster Schritt an, um besser mit den Daten vertraut zu werden. Beschreiben Sie so eine einfache Analyse!
- Beschreiben Sie anschaulich, was ein Histogramm ist und was man daraus lernen kann!
- Erläutern Sie die Unterschiede zwischen linearen bzw. logarithmischen Skalen auf der horizontalen und/oder vertikalen Achse eines Plots!
- Beschreiben Sie kurz, was ein Korrelationskoeffizient ist und was man daraus (nicht) lernen kann!
- Geben Sie ein Beispiel für Daten, bei denen eine Korrelation zu erwarten ist!
- Geben Sie ein Beispiel für Daten, bei denen Sie eine Korrelation überraschen würde!
Fragen zu Grundlagen der Optimierung und Gradient Descent
- Was ist Optimierung?
- Nennen Sie mögliche Einschränkungen für ein Optimierungsproblem!
- Sind Minimierung und Maximierung im Grunde das gleiche Problem oder nicht?
- Beschreiben Sie anschaulich Zweck und Grenzen des “Brute-Force”-Zugangs zu einem Optimierungsproblem!
- Beschreiben Sie ein Beispiel für die iterative Lösung eines Optimierungsproblems!
- Diskutieren Sie die Unterschiede von Optimierungsproblemen mit kontinuierlichen Variablen gegenüber diskreten Optimierungsproblemen!
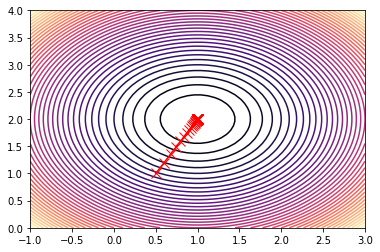
- Wie funktioniert der Gradient-Descent-Algorithmus?
- Welche Einschränkungen gelten für den Gradient-Descent-Algorithmus?
- Schildern Sie, wie Gradient-Descent gut funktionieren kann und woran er scheitern kann!
- Erläutern Sie den Unterschied zwischen einem lokalen und einem globalen Optimum und deren Rolle bei der Verwendung von Gradient-Descent!
Fragen zu Stochastische Optimierung und Genetische Algorithmen
- Woher kommen die (Pseudo-)Zufallszahlen, die wir in Python verwendet haben?
- In NumPy kann man Pseudozufallszahlen aus bestimmten Verteilungen erzeugen lassen. Beschreiben Sie kurz, warum das sinnvoll sein kann!
- Was bedeutet der Begriff “Sampling”?
- Welche Vorteile hat stochastische Optimierung gegenüber Gradient-Descent?
- Warum kann ein Optimierungsverfahren, das auf Pseudozufallszahlen beruht, überhaupt funktionieren?
- Was ist ein Genetischer Algorithmus?
- Wie muss man sich den “Genetischen Code” bei einem Genetischen Algorithmus vorstellen?
- Welche Mechanismen stehen zur Verfügung, um bei einem Genetischen Algorithmus die nächste Generation aus der aktuellen Population zu erzeugen?
- Welche Parameter kann man bei einem Genetischen Algorithmus verändern?
- Findet ein Genetischer Algorithmus immer die bestmögliche Lösung für das Optimierungsproblem?
Fragen zu Monte-Carlo-Methoden – Simulation und Integration
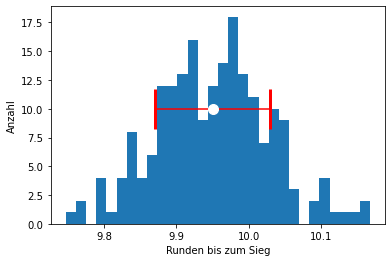
- Beschreiben Sie eine Monte-Carlo-Simulation im Überblick!
- Wie wählen Sie die Anzahl der nötigen Runs für eine gute Monte-Carlo-Simulation?
- Welche Rolle spielen Samples bei einer Monte-Carlo-Simulation?
- Wie hilft der Zentrale Grenzwertsatz bei der Auswertung einer Monte-Carlo-Simulation?
- Warum ist ein einziger Run einer Monte-Carlo-Simulation zu wenig für eine fundierte Aussage zum Verhalten des simulierten Systems?
- Nennen Sie ein Beispiel für ein System, das man gut mit einer Monte-Carlo-Simulation untersuchen kann!
- Welche Größe ist wichtiger, um die Qualität eines Monte-Carlo-Simulations-Resultats einschätzen zu können: Der Mittelwert aller Ergebnisse oder der zugehörige Fehler?
- Wie haben wir auf einfache Art den Wert der Zahl Pi per Monte-Carlo-Simulation abgeschätzt?
- Wie skaliert der Fehler bei der Monte-Carlo-Simulation/Integration mit der Anzahl der Simulations-/Integrations-Punkte?
- Funktioniert Monte-Carlo-Simulation nur für Würfel- oder Kartenspiele?
Fragen zu Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk
- Beschreiben Sie, wie die effiziente Monte-Carlo-Integrationsmethode funktioniert, die wir kennen gelernt haben!
- Worauf muss man achten, wenn man einen Teil eines Integrals als Wahrscheinlichkeitsdichte interpretiert?
- Warum hat die Interpretation eines Teils des Integrals als Wahrscheinlichkeitsdichte einen Vorteil?
- Welche Arten von Integralen kann man mit dieser Art von numerischer Integration lösen?
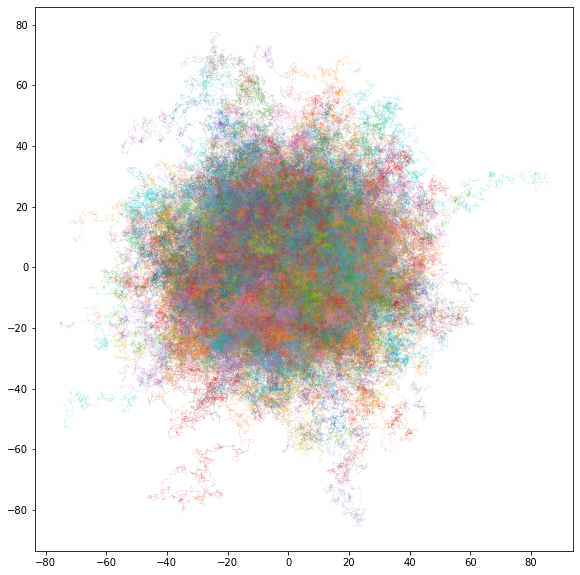
- Was ist ein “Random Walk”?
- Welche Rolle spielt ein Weg (ein Walk) in einer Monte-Carlo-Simulation eines Systems?
- Welche Größen können bei der Analyse von Random Walks interessant sein?
- Welche Parameter können Sie bei einem Random Walk einstellen?
- Welche Parameter sind bei einem Random Walk vorgegeben?
- Nennen Sie ein anschauliches Beispiel für ein System, das sich gut mit einer Monte-Carlo-Simulation über Random Walks untersuchen ließe!
Fragen zu Unsupervised Machine Learning: Clustering von Daten
- Was versteht man im Allgemeinen unter “Machine Learning”?
- Erklären Sie den wesentlichen Unterschied zwischen unsupervised und supervised Learning!
- Wenn Sie fast nichts über einen Datensatz wissen, können Sie dann eher unsupervised oder supervised Learning darauf anwenden?
- Kann unsupervised Learning bei der Datenanalyse helfen? Warum (nicht)?
- Was versteht man unter dem Begriff “Clustering”?
- Welche Parameter beschreiben eine bestimmte Art von Clustering?
- Wie funktioniert hierarchisches bzw. agglomeratives Clustering?
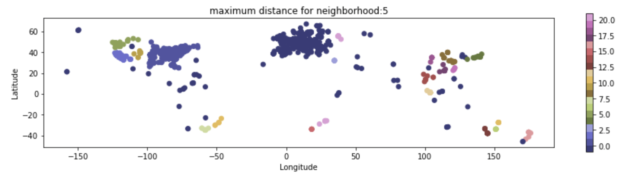
- Wie funktioniert ein dichte-basierter Clustering-Algorithmus und welche Vorteile hat er?
- Wie funktioniert der K-Means Clustering-Algorithmus?
- Nennen Sie ein Beispiel für einen Datensatz und welchen Clustering-Algorithmus Sie am ehesten darauf anwenden würden!
Fragen zu Supervised Machine Learning: Grundlagen
- Wie bezeichnet man Inputs und Outputs beim supervised Learning im Fachjargon?
- Zum Beispiel welche Arten von Labels kann man bei Daten vorfinden?
- Warum ist die Vorbereitung der Daten beim supervised Learning so wichtig?
- Wie sorgt man dafür, dass die Trainingsdaten beim supervised Learning ausgewogen sind, und was bedeutet das?
- Nennen Sie ein paar der typischen Schritte bei der Durchführung von supervised Learning auf einem vorgegebenen Datensatz!
- Was ist beim supervised Learning erfahrungsgemäß schwieriger: Ordentliche Daten zu bekommen oder ein Modell darauf zu trainieren?
- Beschreiben Sie anschaulich die Funktionsweise eines “Decision Trees”.