- Startseite
- Allgemeine Informationen zur Lehrveranstaltung
- Einfaches Python Setup und Wichtige Informationen
- 0. Python Einführung und Checkup
- 1. Einführung und einfache Algorithmen
- 2. Differenzieren und Integrieren
- 3. Vektoren, Matrizen und Vektorisierung in Python
- 4. Datenanalyse bzw. Datenauswertung
- 5. Grundlagen der Optimierung und Gradient Descent
- 6. Stochastische Optimierung und Genetische Algorithmen
- 7. Monte-Carlo-Methoden – Simulation und Integration
- 8. Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk
- 9. Unsupervised Machine Learning: Clustering von Daten
- 10. Supervised Machine Learning: Grundlagen
- 11. Einführung in künstliche neuronale Netzwerke
Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.
4. Datenanalyse bzw. Datenauswertung¶
In dieser Einheit werden wir uns mit den nötigsten Grundlagen der Datenanalyse bzw. Datenauswertung befassen. Das bedeutet z.B., wie man Daten einliest, was man damit (nicht) machen sollte und was man sich alles von Daten erwarten darf und was nicht.
4.1 Dateneinlesen und Selektieren mit Pandas¶
In Python gibt es eine Package, Pandas, die speziell für den einfachen Umgang mit Daten gedacht ist, die in Tabellenform abgelegt sind. Z.B. kann man aus einem Tabellenkalkulationsprogramm ein Arbeitsblatt im csv-Format speichern. CSV steht für Comma-Separated Values und ist ein oft verwendeter Standard, mit dem Sie sicher zumindest ab und zu zu tun haben sollten.
Wir werden hier nicht in die Tiefen von Pandas abtauchen (dafür reicht unsere Zeit nicht), aber ich möchte Ihnen ein paar der wichtigsten Schritte von einem CSV-File zu einem NumPy-Array zeigen. Denn was man damit alles macht, daran werden wir weiterhin arbeiten.
Zunächst die Imports für diese Einheit:
%matplotlib inline
# Lade die Pandas-Package
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
Das zentrale Objekt in Pandas ist ein Dataframe, das im Prinzip Tabellen- bzw. auch Datenbank-Charakter hat. Sie können sich das vereinfacht so vorstellen, dass die Spalten in der Tabelle Namen haben und die Zeilen durchnummeriert sind (so wie in einer Tabellenkalkulation). Wir sehen uns das jetzt gleich einmal an einem Beispiel an.
Ich habe hier für Sie zwei Datensätze von kaggle.com bereitgestellt. Kaggle ist eine Plattform für Machine-Learning Wettbewerbe, und dadurch auch über die Zeit zu einem sehr interessanten Repository für Datensätze geworden (die Registrierung ist kostenlos, falls sich das jemand von Ihnen ansehen möchte).
Zunächst nehmen wir einen Datensatz zur Hand, der zu GeoLifeCLEF 2022 gehört. Dabei geht es darum, anhand von Bildmaterial (mit dem wir uns diesmal allerdings nicht beschäftigen werden) vorherzusagen, welche Spezies von Tieren und Pflanzen an diesem Ort leben. Die Basis dafür ist ein Satz von Trainingsdaten, in denen Beobachtungen von Spezies mit geografischer Länge und Breite gesammelt sind. Diese Liste von Beobachtungen wollen wir einlesen und ein wenig auswerten.
Quelle: https://www.kaggle.com/competitions/geolifeclef-2022-lifeclef-2022-fgvc9/data
# Einlesen des csv-Files in ein Pandas-Dataframe
df_all = pd.read_csv(os.path.join("data","observations_us_train.csv"), delimiter=";")
# Anzeigen der ersten paar Zeilen des Dataframe bzw. der Tabelle.
# Man sieht hier die Spalten-Titel und die Indizes der Zeilen
df_all.head()
| observation_id | latitude | longitude | species_id | subset | |
|---|---|---|---|---|---|
| 0 | 20000173 | 33.197660 | -116.180680 | 4911 | train |
| 1 | 20000175 | 34.037968 | -118.876755 | 4912 | train |
| 2 | 20000176 | 27.620740 | -97.222690 | 4913 | train |
| 3 | 20000177 | 29.155582 | -95.653930 | 4914 | train |
| 4 | 20000179 | 36.605740 | -121.959510 | 4915 | train |
# wir werden nun einige Zeilen aus der Tabelle nehmen,
# und zwar durch Einschränkung auf die species_id
# zunächst definieren wir eine Liste solcher IDs
species_sample = [200, 20, 440, 57, 42, 7346]
# Erzeuge Figur
fig = plt.figure(figsize=(8, 10))
# Loop über Species-ID mit Position in der Liste
for ind_species, a_species in enumerate(species_sample):
# hole aus dem Dataframe jene Zeilen, die die jeweilige species ID haben
df_data_species_sample = df_all[df_all['species_id'] == a_species]
# Erzeuge ein Array zur weiteren Verwendung in numpy
plot_array = np.transpose(df_data_species_sample[['latitude', 'longitude']].to_numpy())
# Erzeuge einen neuen Subplot für diese Spezies
ax = plt.subplot(3, 2, ind_species+1)
# Erzeuge den Plot dieser Beobachtungen bezüglich Länge und Breite
ax.scatter(plot_array[1], plot_array[0])
# Labels für die Achsen
ax.set_xlabel("Longitude")
ax.set_ylabel("Latitude")
# noch die Spezies-ID als Titel in den Subplot
plt.title("spezies "+str(a_species))
plt.show()
# Das sieht noch nicht nach allzuviel aus. Daher plotten
# wir jetzt mal alle Beobachtungen für alle Spezies auf einmal
# Erzeuge Figur
fig = plt.figure()
# Nimm alle Daten in den Spalten 'latitude', 'longitude' und mache
# daraus ein numpy-Array
plot_array = np.transpose(df_all[['latitude', 'longitude']].to_numpy())
# Und ein Scatterplot der Daten. Die point size (s) wird klein gemacht
# für eine schönere Auflösung/Darstellung
plt.scatter(plot_array[1], plot_array[0], s=.0001)
# Achsenbeschriftungen
plt.xlabel("Longitude")
plt.ylabel("Latitude")
# und Plot-Titel
plt.title("Alle Spezies")
plt.show()
4.2 Datenanalyse, erste Schritte¶
Wir werden uns jetzt noch einen anderen Datensatz organisieren, um damit etwas von der üblichen Auswertung anzusehen. Es handelt sich dabei um Ort und Zeit sowie Magnitude der Erdbeben mit $M>5.5$ von 1965 bis 2016.
Quelle: https://www.kaggle.com/datasets/usgs/earthquake-database
Sehen wir uns das einfach mal an:
# Einlesen des csv-Files in ein Pandas-Dataframe
df_eq_all = pd.read_csv(os.path.join("data","earthquake_database.csv"), delimiter=",")
# Anzeigen der ersten paar Zeilen des Dataframe bzw. der Tabelle.
# Man sieht hier die Spalten-Titel und die Indizes der Zeilen
df_eq_all.head()
| Date | Time | Latitude | Longitude | Type | Depth | Depth Error | Depth Seismic Stations | Magnitude | Magnitude Type | … | Magnitude Seismic Stations | Azimuthal Gap | Horizontal Distance | Horizontal Error | Root Mean Square | ID | Source | Location Source | Magnitude Source | Status | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 01/02/1965 | 13:44:18 | 19.246 | 145.616 | Earthquake | 131.6 | NaN | NaN | 6.0 | MW | … | NaN | NaN | NaN | NaN | NaN | ISCGEM860706 | ISCGEM | ISCGEM | ISCGEM | Automatic |
| 1 | 01/04/1965 | 11:29:49 | 1.863 | 127.352 | Earthquake | 80.0 | NaN | NaN | 5.8 | MW | … | NaN | NaN | NaN | NaN | NaN | ISCGEM860737 | ISCGEM | ISCGEM | ISCGEM | Automatic |
| 2 | 01/05/1965 | 18:05:58 | -20.579 | -173.972 | Earthquake | 20.0 | NaN | NaN | 6.2 | MW | … | NaN | NaN | NaN | NaN | NaN | ISCGEM860762 | ISCGEM | ISCGEM | ISCGEM | Automatic |
| 3 | 01/08/1965 | 18:49:43 | -59.076 | -23.557 | Earthquake | 15.0 | NaN | NaN | 5.8 | MW | … | NaN | NaN | NaN | NaN | NaN | ISCGEM860856 | ISCGEM | ISCGEM | ISCGEM | Automatic |
| 4 | 01/09/1965 | 13:32:50 | 11.938 | 126.427 | Earthquake | 15.0 | NaN | NaN | 5.8 | MW | … | NaN | NaN | NaN | NaN | NaN | ISCGEM860890 | ISCGEM | ISCGEM | ISCGEM | Automatic |
5 rows × 21 columns
# außerdem kann man sich für ein Dataframe
# auch ein paar Statistiken anzeigen lassen:
df_eq_all.describe()
| Latitude | Longitude | Depth | Depth Error | Depth Seismic Stations | Magnitude | Magnitude Error | Magnitude Seismic Stations | Azimuthal Gap | Horizontal Distance | Horizontal Error | Root Mean Square | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 23412.000000 | 23412.000000 | 23412.000000 | 4461.000000 | 7097.000000 | 23412.000000 | 327.000000 | 2564.000000 | 7299.000000 | 1604.000000 | 1156.000000 | 17352.000000 |
| mean | 1.679033 | 39.639961 | 70.767911 | 4.993115 | 275.364098 | 5.882531 | 0.071820 | 48.944618 | 44.163532 | 3.992660 | 7.662759 | 1.022784 |
| std | 30.113183 | 125.511959 | 122.651898 | 4.875184 | 162.141631 | 0.423066 | 0.051466 | 62.943106 | 32.141486 | 5.377262 | 10.430396 | 0.188545 |
| min | -77.080000 | -179.997000 | -1.100000 | 0.000000 | 0.000000 | 5.500000 | 0.000000 | 0.000000 | 0.000000 | 0.004505 | 0.085000 | 0.000000 |
| 25% | -18.653000 | -76.349750 | 14.522500 | 1.800000 | 146.000000 | 5.600000 | 0.046000 | 10.000000 | 24.100000 | 0.968750 | 5.300000 | 0.900000 |
| 50% | -3.568500 | 103.982000 | 33.000000 | 3.500000 | 255.000000 | 5.700000 | 0.059000 | 28.000000 | 36.000000 | 2.319500 | 6.700000 | 1.000000 |
| 75% | 26.190750 | 145.026250 | 54.000000 | 6.300000 | 384.000000 | 6.000000 | 0.075500 | 66.000000 | 54.000000 | 4.724500 | 8.100000 | 1.130000 |
| max | 86.005000 | 179.998000 | 700.000000 | 91.295000 | 934.000000 | 9.100000 | 0.410000 | 821.000000 | 360.000000 | 37.874000 | 99.000000 | 3.440000 |
Wir werden allerdings jetzt auf NumPy umsteigen und damit ein paar Dinge auseinandernehmen. Dabei erzeugen wir durch Abfrage einfach einmal ein recht großes NumPy-Array mit im Prinzip all jenen Daten, die wir verwerten wollen. Danach folgt die Analyse einzelner Spalten oder auch verschiedener möglicher Zusammenhänge.
# die Spalten, die uns interessieren:
column_labels = ['Date', 'Time', 'Latitude', 'Longitude', 'Depth', 'Depth Error',
'Magnitude', 'Magnitude Error', 'Horizontal Error', 'Root Mean Square']
# Schränke Typ auf Erdbeben ein (es gibt nämlich auch nukleare Explosionen)
df_eq_data = df_eq_all[df_eq_all['Type'] == "Earthquake"]
# Erzeuge gesamt-Daten-Array
eq_data = df_eq_data[column_labels].to_numpy()
# Erzeuge Figur
fig = plt.figure()
# Nimm alle Daten in den Spalten 'latitude', 'longitude' und transponiere
# wieder das numpy-Array fürs Plotten
plot_array = np.transpose(eq_data[:, 2:4])
# Und ein Scatterplot der Daten. Die point size (s) wird klein gemacht
# für eine schönere Auflösung/Darstellung
plt.scatter(plot_array[1], plot_array[0], s=.001)
# Achsenbeschriftungen
plt.xlabel("Longitude")
plt.ylabel("Latitude")
# und Plot-Titel
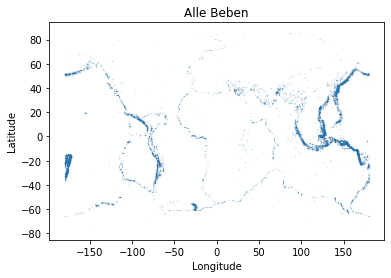
plt.title("Alle Beben")
plt.show()
# Versuchen wir das nochmal, in 3D
from mpl_toolkits.mplot3d import Axes3D
# hole Daten, diesmal Länge, Breite, Tiefe
[breiten, laengen, tiefen] = np.transpose(eq_data[:, 2:5].astype(float))
fig = plt.figure()
ax = fig.add_subplot(1,1,1, projection='3d')
# Und ein Scatterplot der Daten. Die point size (s) wird klein gemacht
# für eine schönere Auflösung/Darstellung
ax.scatter(laengen, breiten, tiefen, s=.001)
# Achsenbeschriftungen
plt.xlabel("Longitude")
plt.ylabel("Latitude")
#plt.zlabel("Depth")
# und Plot-Titel
plt.title("Alle Beben")
plt.show()
# und wie wäre es, diesen Plot so aussehen zu lassen, wie eine Erdkugel?
r_earth = 6370 # in km
x_values = (r_earth - tiefen*5) * np.cos(breiten/180*np.pi) * np.cos(laengen/180*np.pi)
y_values = (r_earth - tiefen*5) * np.cos(breiten/180*np.pi) * np.sin(laengen/180*np.pi)
z_values = (r_earth - tiefen*5) * np.sin(breiten/180*np.pi)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Und ein Scatterplot der Daten. Die point size (s) wird klein gemacht
# für eine schönere Auflösung/Darstellung
ax.scatter(x_values, y_values, z_values, s=.001)
# und Plot-Titel
plt.title("Alle Beben, Tiefe fünffach eingezeichnet")
plt.show()
4.3 Einfache statistische Auswertung¶
Nachdem wir uns die Daten angesehen und ein Gefühl dafür entwickelt haben, möchten wir uns aber noch ein paar quantitative Eigenschaften ansehen. Z.B. wollen wir versuchen, Mittelwerte und Standardabweichungen etwas genauer unter die Lupe zu nehmen.
Die Basis dafür ist wieder NumPy, mit dem Array, das wir schon oben gebaut haben.
# berechne zunächst die arithmetischen Mittelwerte.
# Zur Erinnerung: Spalten ab 2 sind numerisch, gemittelt wird über die Zeilen
np.mean(eq_data[:, 2:].astype(float), axis=0)
array([ 1.38638254, 39.74604874, 71.31391348, nan, 5.88276257,
nan, nan, nan])# Hier gibt es offenbar einige NaNs, d.h. "not a number".
# NumPy hat dafür eine spezielle mean-Funktion, die NaNs auslässt
the_means = np.nanmean(eq_data[:, 2:].astype(float), axis=0)
the_means
array([1.38638254e+00, 3.97460487e+01, 7.13139135e+01, 4.92132277e+00,
5.88276257e+00, 6.61968254e-02, 6.70467570e+00, 1.02351759e+00])# Machen wir das gleiche auch noch für die Standardabweichungen
the_stds = np.nanstd(eq_data[:, 2:].astype(float), axis=0)
the_stds
array([2.99284158e+01, 1.25749196e+02, 1.22965738e+02, 4.68082779e+00,
4.24022662e-01, 3.95287236e-02, 4.62738222e+00, 1.86940996e-01])# jetzt können wir hübsch herausschreiben, was passiert:
# Spalten-Überschriften mit den Mittelwerten und Standardabweichungen
for an_index, a_label in enumerate(column_labels[2:]):
print("Mittelwert für", a_label, ":", round(the_means[an_index], 3), "+-", round(the_stds[an_index], 3))
Mittelwert für Latitude : 1.386 +- 29.928 Mittelwert für Longitude : 39.746 +- 125.749 Mittelwert für Depth : 71.314 +- 122.966 Mittelwert für Depth Error : 4.921 +- 4.681 Mittelwert für Magnitude : 5.883 +- 0.424 Mittelwert für Magnitude Error : 0.066 +- 0.04 Mittelwert für Horizontal Error : 6.705 +- 4.627 Mittelwert für Root Mean Square : 1.024 +- 0.187
Hier sehen wir ein paar seltsame Dinge, z.B. große Fehlerbalken bei kleinen Mittelwerten. Das ist allerdings bei Länge und Breite kein Wunder (denn das sind ja recht beliebige Koordinaten). Bei der Tiefe ist es allerdings schon etwas interessanter. Am besten sehen wir uns die Verteilung ein paar dieser Größen im Detail an.
# Nimm die Tiefenwerte und erstelle ein Histogramm
depth_values = eq_data[:, 4]
plt.figure()
# Histogramm der Tiefenwerte
plt.hist(depth_values, bins=100)
# Achsenbeschriftungen
plt.xlabel("Tiefe in km")
plt.ylabel("Anzahl Beben")
# Skaliere x und/oder y Achse um
#plt.xscale("log")
plt.yscale("log")
plt.show()
# Nehme nun die Magnituden und erstelle ein Histogramm
mag_values = eq_data[:, 6]
# Berechne die Anzahl der Bins für das Histogramm so, dass
# jede zehntel-Magnitude ein Bin wird
num_bins = int((np.max(mag_values) - np.min(mag_values))*10)
# Ausgabe zum Mitschauen
print("num_bins: ", num_bins)
plt.figure()
# Histogramm der Magnituden
plt.hist(mag_values, bins=num_bins)
# Achsenbeschriftungen
plt.xlabel("Magnitude")
plt.ylabel("Anzahl Beben")
# Skaliere x und/oder y Achse um
#plt.xscale("log")
plt.yscale("log")
plt.show()
num_bins: 36
4.4 Etwas komplexere statistische Auswertung¶
Um noch etwas mehr Erfahrungen mit den Daten zu sammeln, wollen wir noch eins überprüfen, nämlich, ob Teile der Daten korreliert sind. Z.B. könnte man sich fragen, ob die Tiefe eines Erdbebens mit der Magnitude zusammenhängt.
Das wollen wir uns anhand des Pearson-Korrelations-Koeffizienten ansehen. Dieser ist 1, wenn eine perfekte Korrelation vorliegt, -1 bei einer Antikorrelation, und 0 bedeutet, dass es keine Korrelation gibt.
np.corrcoef(mag_values.astype(float), depth_values.astype(float))
array([[1. , 0.02322161],
[0.02322161, 1. ]])# was it mit Längen und Breiten?
np.corrcoef(eq_data[:, 2].astype(float), eq_data[:, 3].astype(float))
array([[1. , 0.20267683],
[0.20267683, 1. ]])4.5 Übungsaufgabe: Beben einer bestimmten Region¶
In dieser Übungsaufgabe wollen wir die Korrelation von Längen und Breiten einiger Erdbeben nochmal ansehen, und zwar eingeschränkt auf eine bestimmte Region. Machen Sie also folgendes:
- Nehmen Sie aus dem Daten-Array oben die Zeilen heraus (und kopieren Sie diese in ein neues Array), wo Längen und die Breiten in folgenden Fenstern liegen:
- Länge zwischen 165 und 171 Grad
- Breite zwischen -10 und -24 Grad
- Berechnen Sie für das neue Array die Mittelwerte und Standardabweichungen für Tiefe und Magnitude. Wie vergleichen diese sich mit den obigen Werten für alle Beben?
- Berechnen Sie die Korrelation zwischen Länge und Breite für diesen Teil der Daten. Was können Sie feststellen?
Zusatzaufgabe (optional): Kopieren Sie die Grafische 3D-Darstellung von oben und erzeugen Sie diese für das eingeschränkte Datenset. Nehmen Sie hierbei die Magnitude zur Hand und färben Sie darüber die Punkte im Plot verschieden ein. Das geht, indem Sie ein Array von Farbcodes mit c=colorarray im scatter Befehl zusätzlich zu den Koordinaten übergeben.
# zur Erinnerung
column_labels = ['Date', 'Time', 'Latitude', 'Longitude', 'Depth', 'Depth Error',
'Magnitude', 'Magnitude Error', 'Horizontal Error', 'Root Mean Square']
# erzeuge leere Listen zum Anhängen von Werten
# für Daten
restricted_data = []
# für Farben bezüglich der Magnitude
color_strings = []
# Loop über alle Daten, Spalten "Latitude" bis "Magnitude"
for a_line in eq_data[:, 2:7]:
# Abfrage der Koordinatenbereiche
if (165 < a_line[1] < 171) and (-10 > a_line[0] > -24):
# hänge Zeile an die Liste der eingeschränkten Daten an
restricted_data.append(a_line.astype(float))
# setze Farbwerte für 3 Bereiche in der Magnitude
if a_line[4] > 7.5:
color_strings.append("r")
elif a_line[4] > 6.5:
color_strings.append("g")
else:
color_strings.append("b")
# mache aus dem Ganzen wieder ein Array
restricted_data = np.array(restricted_data)
# übergebe das transponierte Array in die 4 interessanten Listen
[breiten, laengen, tiefen, _, magnituden] = np.transpose(restricted_data)
# gib die Minima und Maxima der Magnituden aus, um zu wissen,
# wo die Gruppen von Magnituden-Werten sind
print("Max Magnitude: ", np.max(magnituden))
print("Min Magnitude: ", np.min(magnituden))
# Mittelwerte und Standardabweichungen für reduzierte Daten
print("Tiefe:", round(np.mean(tiefen), 3), "+-", round(np.std(tiefen), 3))
print("Magnitude:", round(np.mean(magnituden), 3), "+-", round(np.std(magnituden), 3))
# gib den Korrelations
np.corrcoef(breiten, laengen)
Max Magnitude: 8.0 Min Magnitude: 5.5 Tiefe: 60.058 +- 69.44 Magnitude: 5.937 +- 0.458
array([[ 1. , -0.92042053],
[-0.92042053, 1. ]])Bei der durchschnittlichen Tiefe sieht man das gleiche Muster: Dort gibt es immer noch eine große Standardabweichung im Vergleich zum Mittelwert.
Die (Anti-)Korrelation zwischen Länge und Breite ist allerdings sehr hoch. Wenn Sie sich die fragliche Region ansehen, werden Sie feststellen, dass sich dort tatsächlich eine lineare Erdbebenzone befindet.
# Hier noch der Erdkugelplot für die eingeschränkten Daten
# Erdradius, nochmal zur Sicherheit
r_earth = 6370 # in km
# Die Koordinaten werden neu berechnet, aus dem eingeschränkten Datenset,
# und diesmal ohne Faktor bei den Tiefen
x_values = (r_earth - tiefen) * np.cos(breiten/180*np.pi) * np.cos(laengen/180*np.pi)
y_values = (r_earth - tiefen) * np.cos(breiten/180*np.pi) * np.sin(laengen/180*np.pi)
z_values = (r_earth - tiefen) * np.sin(breiten/180*np.pi)
# wieder die 3D-Figur
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Und ein Scatterplot der Daten. Die point size (s) machen wir
# diesmal groß, damit man die Farb-Unterschiede besser sieht
ax.scatter(x_values, y_values, z_values, s=1, c=color_strings)
# und Plot-Titel
plt.title("Eingeschränkte Beben, Tiefe realistisch")
# können Sie die roten und grünen Punkte entdecken?
plt.show()