- Startseite
- Allgemeine Informationen zur Lehrveranstaltung
- Einfaches Python Setup und Wichtige Informationen
- 0. Python Einführung und Checkup
- 1. Einführung und einfache Algorithmen
- 2. Differenzieren und Integrieren
- 3. Vektoren, Matrizen und Vektorisierung in Python
- 4. Datenanalyse bzw. Datenauswertung
- 5. Grundlagen der Optimierung und Gradient Descent
- 6. Stochastische Optimierung und Genetische Algorithmen
- 7. Monte-Carlo-Methoden – Simulation und Integration
- 8. Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk
- 9. Unsupervised Machine Learning: Clustering von Daten
- 10. Supervised Machine Learning: Grundlagen
- 11. Einführung in künstliche neuronale Netzwerke
Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.
2. Differenzieren und Integrieren¶
In dieser Einheit werden wir uns mit den Bereichen der Analysis aus der fortgeschrittenen Mathematik beschäftigen. Außerdem werden wir uns mit zwei Herangehensweisen zu konkreten Problemen befassen:
- Der Methode der analytischen Lösungen und
- Numerischen Lösungsmethoden
Ich möchte versuchen, Ihnen auf relativ direktem Weg alles an Werkzeugen in die Hand zu geben, das Sie brauchen werden, um bereits ein sehr breites Spektrum an Problemstellungen angehen zu können. Dabei achten wir darauf, dass Sie Lernen, auf die Mächtigkeit von Python-Bibliotheken zu vertrauen und darauf, dass für nahezu jedes algorithmische oder numerische Problem bereits eine hilfreiche Bibliothek oder Package existiert.
2.1 Analytisches Arbeiten mit Funktionen in SymPy¶
Beginnen wir mit dem eigentlich recht kurzen analytischen Teil. Dafür gibt es in Python die Package SymPy, mit der Sie z.B. die Ableitungen von Funktionen analytisch bestimmen können.
Hinweis: SymPy an sich ist allerdings sehr mächtig und beherrscht wesentlich mehr als wir für die Zwecke dieser Lehrveranstaltung verwenden werden. Da ich Ihnen das nicht vorenthalten möchte (weil es für viele Dinge interessant ist, die mit symbolischen Rechnungen zu tun haben), finden Sie hier, verlinkt, die Dokumentation von SymPy.
2.1.1 Grundbegriffe¶
Zunächst muss man sich noch um die Begriffe der Funktion und der Variablen kümmern und darum, wie diese in Sympy umgesetzt sind. Nehmen wir zu Anfang einfach eine Funktion $f$ einer Variablen $x$, also $f(x)$. Dann haben wir folgendes:
# importiere die Package SymPy
import sympy as sp
# enable prettier Symbol Layout (LaTeX)
sp.init_printing()
# Definiere eine Variable, dafür gibt es die Klasse Symbol
x = sp.Symbol("x")
# wie sieht das aus?
print(x)
# definiere eine Funktion
f = sp.sin(x)
# und wie sieht das aus?
print(f)
x sin(x)
# wenn man eine Funktion an einem bestimmten Wert haben möchte, macht man
print("Der Sinus von", sp.pi, "ist", f.subs(x, sp.pi))
# man substituiert also für das Symbol den Wert. Nochmal:
print(f.subs(x, 1.))
Der Sinus von pi ist 0 0.841470984807897
# Auch mehrere Variablen sind kein Problem
x0, a, z = sp.symbols("x0 alpha z")
# die Ausgabe im Notebook ohne print-Befehl sieht dann wie Formelschrift aus
x0, a, z
# es gibt auch noch eine praktische Kurzschreibweise für gleich eine ganze Reihe von Variablen
abunchofsymbols = sp.symbols("x0:15")
abunchofsymbols
# Man kann mit .subs auch einen Ausdruck in den anderen einsetzen.
# definieren wir noch eine Funktion
g = sp.exp(-x**2)
# und dann setzen wir f in g ein
out_sub = g.subs(x, f)
# wie sieht das aus?
out_sub
# und zu guter letzt brauchen wir eventuell auch mal numerische Werte:
# aus
out_sub.subs(x, 4)
# wird
sp.N(out_sub.subs(x, 4))
# das gilt auch für die Konstanten
sp.N(sp.pi, 400)
# und hier noch eine effiziente Möglichkeit für Arrays
# importieren von Numpy
import numpy as np
# ein Array, z.B. für einen Plot (als x-Werte)
x_values = np.linspace(0, 30, 30)
# so kann man die Werte im Array auf einmal zu numerischen Werten in einem f-Array machen
# Vorbereitung der "Funktion für das Einsetzen eines Arrays"
g_to_numerical = sp.lambdify(x, g)
# das Einsetzen des Arrays:
g_to_numerical(x_values)
array([1.00000000e+000, 3.42955500e-001, 1.38341057e-002, 6.56356739e-005,
3.66272534e-008, 2.40405446e-012, 1.85592231e-017, 1.68519759e-023,
1.79977167e-030, 2.26078642e-038, 3.34023640e-047, 5.80457487e-057,
1.18642195e-067, 2.85222298e-079, 8.06498047e-092, 2.68224664e-105,
1.04922745e-119, 4.82743150e-135, 2.61239078e-151, 1.66278350e-168,
1.24482648e-186, 1.09611841e-205, 1.13522427e-225, 1.38287017e-246,
1.98132946e-268, 3.33893163e-291, 6.61810876e-315, 0.00000000e+000,
0.00000000e+000, 0.00000000e+000])2.1.2 Lösen von Gleichungen¶
SymPy kann auch verwendet werden, um Gleichungen zu lösen. Dazu muss man zunächst eine Gleichung definieren. Das geht mit einem separaten Befehl, da = und == bereits anderweitig belegt sind (nämlich mittels sp.Eq). Danach kann man die Lösung der Gleichung finden (mit sp.solveset). Hier die einzelnen Schritte im Detail.
# Definieren einer Gleichung
sp.Eq(x, z)
# oder mit den Befehlen von vorher
sp.Eq(f, g)
# Bei Angabe nur eines Arguments passiert folgendes:
sp.Eq(f)
/Users/ank/opt/anaconda3/lib/python3.8/site-packages/sympy/core/relational.py:486: SymPyDeprecationWarning: Eq(expr) with rhs default to 0 has been deprecated since SymPy 1.5. Use Eq(expr, 0) instead. See https://github.com/sympy/sympy/issues/16587 for more info. SymPyDeprecationWarning(
# das sieht man allerdings in älteren Tutorials teilweise.
# Stattdessen soll man also schreiben
sp.Eq(f, 0)
# Lösen einiger Gleichungen
# zunächst: endlich viele Lösungen
sol = sp.solveset(sp.Eq(x**2, 2))
sol
# Verwendbar sind die Lösungen z.B. als Liste
sp.N(list(sol)[0], 5)
# aber auch: unendlich viele Lösungen:
sp.solveset(sp.Eq(f, 0))
# oder aber auch: keine Lösungen im Reellen, dafür im Komplexen:
sp.solveset(sp.Eq(f + sp.pi, 0))
2.1.3 Differenzieren in SymPy¶
Als nächstes sehen wir uns nun konkret das Differenzieren an. Die Funktionalität hierbei ist sehr intuitiv. Alles was an Symbolen in einem Ausdruck enthalten ist, kann als Differentiationsvariable verwendet werden. Hier zunächst ein sehr einfaches Beispiel, danach ein paar weitere, damit Sie die Möglichkeiten sehen. der Befehl zum Ableiten heißt sp.diff().
# zur Erinnerung, eine unserer Funktionen
f
# und hier die Ableitung nach x
sp.diff(f, x)
# und hier die 2. Ableitung nach x
sp.diff(f, x, 2)
# und hier die ersten 10 Ableitungen nach x
for der_i in range(10):
print(sp.diff(f, x, der_i+1))
cos(x) -sin(x) -cos(x) sin(x) cos(x) -sin(x) -cos(x) sin(x) cos(x) -sin(x)
# und hier die Ableitung nach z
sp.diff(f, z)
# mit mehreren Variablen kann man so arbeiten
h = f * f.subs(x, z)
h
# jetzt kann man konbinieren
sp.diff(h, x, z, x)
# jetzt kann man konbinieren
sp.diff(h, x, 3, z, 4, x, 2)
2.1.4 Integrieren in SymPy¶
Auch symbolisches Integrieren ist mit SymPy sehr intuitiv. Der Befehl dazu heißt sp.integrate(), und wir sehen uns am besten auch hier einfach ein paar Beispiele an:
# einfaches unbestimmtes Integral
sp.integrate(f, x)
# Achtung, SymPy gibt nicht automatisch die Integrationskonstante dazu
# das muss man also selbst machen:
C = sp.Symbol("C")
sp.integrate(f, x) + C
# der gleiche Befehl funktioniert auch für ein Bestimmtes Integral:
sp.integrate(f, (x, 0, sp.pi))
# noch ein bestimmtes Integral
sp.integrate(1/sp.sqrt(2 * sp.pi) * sp.exp(-x**2 / 2), (x, -sp.oo, sp.oo))
# und hier noch ein mehrfach-Integral.
# Zunächst die Variablen für die Integration
r, theta, phi = sp.symbols("r theta phi")
r, theta, phi
# und nun z.B. die Berechnung des Volumens der Einheitskugel
sp.integrate(r**2 * sp.sin(theta), (r, 0, 1), (theta, 0, sp.pi), (phi, 0, 2*sp.pi))
# hier ein Beispiel für ein nicht lösbares Integral, zunächst unbestimmt
unsolvable = sp.sin(sp.exp(-x**5)/x**2)
sp.integrate(unsolvable, x)
# dann bestimmt (das sehen wir uns weiter unten nochmals an)
sp.integrate(unsolvable, (x, 1, 2))
2.2 Numerische Verfahren¶
2.2.1 Numerisches Ableiten im Allgemeinen¶
Zunächst sehen wir uns einmal an, wie man eigentlich eine Funktion numerisch ableitet. Genauer gesagt, sehen wir uns an, wie man den Wert der Ableitung einer Funktion an einer bestimmten Stelle numerisch berechnen kann. Dafür gibt es grundsätzlich ein Prinzip, nämlich das des Differenzenquotienten. Diesen schreibt man üblicherweise als
$\frac{f(x+h)-f(x)}{h}$
wobei $h$ ein kleiner Abstand zwischen zwei Punkten ist. Aus dieser Formel ist allerdings klar, dass diese Steigung (einer Sekante mit einem Punkt an jener Stelle, wo man die Ableitung bestimmen möchte) erst im Limes mit der Tangente übereinstimmt (das ist ja auch die Definition des Differentialquotienten). Numerisch gesehen kann man das jedoch nicht erreichen (sonst dividiert man irgendwann durch 0). Somit erzeugt diese Art, die Ableitung numerisch zu bestimmen, einen numerischen Fehler.
Je nach gewünschter Genauigkeit ist es daher hilfreich, mehrere Terme zu kombinieren und so den numerischen Fehler zu reduzieren. Die einfachste Möglichkeit dafür ist eine symmetrische Version des Differenzenquotienten zu nehmen:
$\frac{f(x+h)-f(x-h)}{2h}$
Wenn man sich diesen Ausdruck und die zugehörige Sekante durchdenkt, wird rasch intuitiv klar, dass deren Steigung wesentlich besser der Tangentensteigung entspricht. Durch die Hinzunahme noch weiterer Terme wird der numerische Fehler immer kleiner. Wir wollen uns allerdings nicht unbedingt mit solchen Dingen befassen, sondern damit, wie wir in Python numerisch differenzieren können.
Nehmen wir also z.B. die zweite Formel her und setzen diese in Python für ein einfaches NumPy-Array um:
# ein paar x-Werte
x_vals = np.linspace(1, 4, 50)
# dazu eine Funktion, sagen wir x^3
xcubed_vals = x_vals ** 3
# dann die Funktion für die Ableitung
# zunächst definieren wir h
h_param = 1.e-5
# dann die symmetrische Formel
numerical_diff_xcubed = ((x_vals + h_param)**3 - (x_vals - h_param)**3) / 2 / h_param
%matplotlib inline
import matplotlib.pyplot as plt
# sehen wir uns das kurz an
# Erzeuge Figur
fig = plt.figure()
plt.plot(x_vals, xcubed_vals, label=r"$x^3$")
plt.plot(x_vals, numerical_diff_xcubed, label=r"$3x^2$")
plt.legend(loc=0)
plt.show()
Das ist zwar alles schön und gut, aber wieso brauchen wir das denn eigentlich? Wir könnten ja genauso gut die Ableitung von $x^3$ berechnen, programmieren (oder mit SymPy berechnen lassen), und dann numerisch auswerten, denn die Ableitung einer Funktion kann man ja immer berechnen.
Das gilt allerdings nicht mehr so einfach, wenn man die Funktion nicht in geschlossener Form kennt, oder einfach irgendwelche Daten “geschenkt” bekommt, mit denen man arbeiten soll. Z.B. ein verrauschtes Signal, das wir jetzt einfach einmal folgendermaßen nachstellen wollen:
# die x-Werte von vorhin
x_vals = np.linspace(1, 4, 50)
# dazu eine Funktion, sagen wir x^3, aber mit Zufallszahlen dazuaddiert
xcubed_vals = x_vals ** 3 + 0.7 * np.random.random(size=(len(x_vals)))
# dann die Funktion für die Ableitung
# zunächst definieren wir h
h_param = 1.e-5
# die symmetrische Formel muss an dieser Stelle etwas anders geschrieben werden
numerical_diff_xcubed = ((x_vals + h_param)**3 + 0.7 * np.random.random(size=(len(x_vals)))
- (x_vals - h_param)**3 - 0.7 * np.random.random(size=(len(x_vals)))) / 2 / h_param
# sehen wir uns auch das kurz an
# Erzeuge Figur
fig = plt.figure()
plt.plot(x_vals, xcubed_vals, label=r"$x^3$")
plt.plot(x_vals, numerical_diff_xcubed, label=r"$3x^2$")
plt.legend(loc=0)
plt.show()
Das sieht relativ chaotisch aus, und das ist es auch. Die großen Änerungen in der Ableitung kommen von den Zufallstermen und daher, dass der Abstand zwischen zwei nebeneinanderliegenden Werten sehr klein ist. Nehmen wir also $h$ etwas größer an, und plotten wir diese Darstellung für verschiedene Werte.
# die x-Werte von vorhin
x_vals = np.linspace(1, 4, 50)
# dazu eine Funktion, sagen wir x^3, aber mit Zufallszahlen dazuaddiert
xcubed_vals = x_vals ** 3 + 0.7 * np.random.random(size=(len(x_vals)))
# Erzeuge Figur
fig = plt.figure(figsize=(15, 20))
# hier nun der Loop über verschiedene Werte von h
for ind_param, h_param in enumerate([1.e-5, 1.e-4, 1.e-3, 1.e-2, 1.e-1, .5]):
ax = plt.subplot(3, 2, ind_param+1)
# die symmetrische Formel muss an dieser Stelle etwas anders geschrieben werden
numerical_diff_xcubed = ((x_vals + h_param)**3 + 0.7 * np.random.random(size=(len(x_vals)))
- (x_vals - h_param)**3 - 0.7 * np.random.random(size=(len(x_vals)))) / 2 / h_param
# plotten der beiden Kurven
ax.plot(x_vals, xcubed_vals, label=r"$x^3$")
ax.plot(x_vals, numerical_diff_xcubed, label=r"$3x^2$")
# plt.legend(loc=0)
plt.show()
So sehen wir, dass man auf die numerische Genauigkeit (Rauschen) und auf den Abstand zwischen den Punkten achten muss. Manchmal kann man sich jedoch beides nicht wirklich aussuchen und muss mit jener Qualität arbeiten, die man zur Verfügung hat.
2.2.2 Numerisches Ableiten in Python¶
Es ist gut, dass Sie jetzt wissen, wie man eine numerische Ableitung berechnet und programmiert. Doch dabei wollen wir es in der Praxis belassen. Denn es ist nicht nötig, jedes mal so einen Aufwand zu betreiben, wenn Sie numerisch differenzieren wollen. Also holen wir uns jetzt die nötige Funktionalität einfach an Bord.
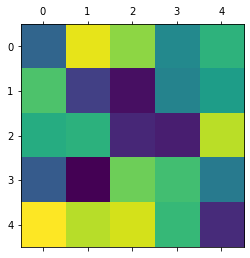
Dazu verwenden wir die Package NumPy, die wir bereits kennen und die uns noch viel Freude machen wird. Der Befehl für eine Ableitung in numpy ist np.gradient(). Das Praktische: Das funktioniert auch in mehreren Dimensionen.
# ein Beispiel für ein Array, wieder einmal zufällig gewählt:
data_array = np.random.random(size=(200, 200))
# und hier die Ableitung in alle Richtungen
data_derivative = np.gradient(data_array)
# Erzeuge eine Figur
fig=plt.figure(figsize=(15,10))
# erster Subplot: das 2x2 array
ax1 = plt.subplot(131)
ax1.matshow(data_array)
# zweiter Subplot: die Ableitung des Arrays entlang der einen Koordinate
ax2 = plt.subplot(132)
ax2.matshow(data_derivative[0])
# dritter Subplot: die Ableitung des Arrays entlang der anderen Koordinate
ax3 = plt.subplot(133)
ax3.matshow(data_derivative[1])
plt.show()
2.2.3 Numerische Integration im Allgemeinen¶
Auch und vor allem Integration wird sehr oft numerisch gemacht. Das kommt einerseits daher, dass man ja nicht alle Funktionen analytisch integrieren kann (im Gegensatz dazu, dass man alle in einer geschlossenen Form angeschriebenen Funktionen grundsätzlich analytisch differenzieren kann).
Für numerisches Integrieren gibt es mehrere Möglichkeiten. An dieser Stelle befassen wir uns erst einmal mit der einfachsten Methode, der Trapezregel. Die Monte-Carlo-Integration kommt an einer späteren Stelle zum Einsatz.
Die Trapezregel hat ihren Namen von der konkreten Art und Weise, wie man Trapeze zum Annähern des Integrals benutzt. Dabei wird die Fläche unter der Kurve zwischen zwei Punkten $a$ und $b$ durch jenes Trapez angenähert, das entsteht, wenn man die Punkte $a$ und $b$ auf der $x$-Achse, sowie die Punkte $f(a)$ und $f(b)$ durch gerade Linien verbindet.
2.2.4 Numerische Integration in Python¶
Wieder gilt: Um sich selbst nicht zu sehr in Programmier-Details zu verstricken, verwenden wir in der Praxis am besten Bibliotheken. Die NumPy-Package hält auch die Trapezregel als np.trapz() für uns bereit, sodass wir z.B. das nicht direkt lösbare Integral von oben nun numerisch angehen können:
# numpy.trapz() braucht ein Array von y-Werten
# dazu generiern wir zuerst einige x-Werte auf unserem Integrationsintervall [1, 2]
a = 1
b = 2
# und bereite y-Werte vor
y_num = sp.lambdify(x, unsolvable)
# hier ein for-Loop über verschiedene Werte für die Anzahl
# der Integrationspunkte oder "Stützstellen"
for n_points in [2, 5, 10, 20, 200, 2000, 20000, 200000]:
# definiere den Abstand zwischen zwei Punkten
del_x = (b-a)/n_points
# Erzeuge n_points x-Werte von a bis b
x_values = np.linspace(a, b, n_points)
# rechne y-Werte aus
y_values = y_num(x_values)
# Berechne das numerische Integral mit der Trapezregel
# und gib das Resultat sowie die Anzahl der verwendeten Punkte aus
# np.trapz braucht hier y-Werte und den Abstand zwischen den x-Werten, nicht mehr
print(np.trapz(y_values, dx=del_x), "für", n_points, "Integrationspunkte.")
0.08990939135312469 für 2 Integrationspunkte. 0.04205889755944999 für 5 Integrationspunkte. 0.03812196787287553 für 10 Integrationspunkte. 0.03841129038496632 für 20 Integrationspunkte. 0.039683503296625115 für 200 Integrationspunkte. 0.03985797261542538 für 2000 Integrationspunkte. 0.039875868069121696 für 20000 Integrationspunkte. 0.03987766207727303 für 200000 Integrationspunkte.
# wie sieht diese Funktion eigentlich aus?
fig = plt.figure()
# nimm die zuletzt verwendeten y-Werte und plotte sie
plt.plot(x_values, y_values)
plt.title(unsolvable)
plt.show()
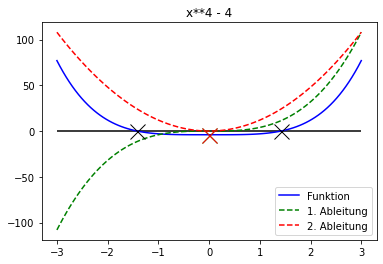
2.3 Übungsaufgabe: Kurvendiskussion¶
Wir werden nun diese Methoden auf etwas anwenden, das Ihnen bekannt vorkommen sollte: Die Kurvendiskussion. Als Beispielfunktion nehmen wir ein Polynom 3. Grades, und zwar: $p(x)=x^3+x^2-2x+4$. Sie sollen damit folgendes tun:
- Definieren Sie das Polynom als Funktion in SymPy, und zwar als Funktion des SymPy-Symbols x
- Verwenden Sie Matplotlib, um eine grafische Darstellung der Funktion im Bereich -3 bis 3 zu machen
- Um die Daten für das Plotten zu bekommen, werten Sie die symbolische Funktion numerisch aus und erzeugen Sie so ein NumPy-Array
- Finden Sie mit SymPy die Nullstellen des Polynoms mittels solveset
- Finden Sie symbolisch die ersten beiden Ableitungen
- Finden Sie mit SymPy die Nullstellen der ersten beiden Ableitungen
- Stellen Sie die Ableitungen zusammen mit der Funktion in einem Plot dar
- Markieren Sie im Plot auf der Funktion die Positionen der Nullstellen, Extremwerte und Wendepunkte
Zusatzaufgabe (optional): Verpacken Sie diese Funktionalität so in eine Python-Funktion, dass Sie dieser Funktion nur einen SymPy-Ausdruck, eine Variable (ein Symbol) und eine Plotbereich (ein NumPy-Array, z.B. einen Linspace) übergeben müssen, und der Rest automatisch gemacht wird. Probieren Sie Ihre Funktion für verschiedene SymPy-Ausdrücke (also Kurven) aus.
# Vorbereitungen und das Polynom
# die x-Werte zum Plotten
x_vals = np.linspace(-3, 3, 100)
# das Polynom in SymPy
p = x**3 + x**2 - 2 * x + 4
p
# verpacke alles in eine Funktion von
# x als Symbol, p als Sympy Expression, x_vals als Plot-Domain
def perform_curve_sketching(p, x, x_vals):
# Polynom für Arrays bereit machen
poly_num = sp.lambdify(x, p)
# die Werte von p an den x-Stellen
p_vals = poly_num(x_vals)
# Die erste und zweite Ableitung
p_1 = sp.diff(p, x)
p_2 = sp.diff(p, x, 2)
# vorbereiten auf numerische Ausgabe
p_1_num = sp.lambdify(x, p_1)
p_2_num = sp.lambdify(x, p_2)
# die numerischen Werte für die Plots
p_1_vals = p_1_num(x_vals)
p_2_vals = p_2_num(x_vals)
# finde die Nullstellen der Funktion
zeros = list(sp.N(sp.solveset(sp.Eq(p, 0), domain=sp.Reals)))
# diese Lösungen sollten alle reell sein
# finde Extremwerte und Wendepunkte über Nullstellen der Ableitungen
extrema = list(sp.N(sp.solveset(sp.Eq(p_1, 0), domain=sp.Reals)))
inflection_points = list(sp.N(sp.solveset(sp.Eq(p_2, 0), domain=sp.Reals)))
# Erzeuge neue Figur
fig = plt.figure()
# zeichne Funktion
plt.plot(x_vals, p_vals, "b", label="Funktion")
# Zeichne 1. Ableitung
plt.plot(x_vals, p_1_vals, "g--", label="1. Ableitung")
# Zeichne 2. Ableitung
plt.plot(x_vals, p_2_vals, "r--", label="2. Ableitung")
# Zeichne Nullstellen als X
for a_zero in zeros:
plt.plot(a_zero, 0, "kx", markersize=15)
# Zeichne Extremstellen als X
for one_ex in extrema:
plt.plot(one_ex, sp.N(p.subs(x, one_ex)), "gx", markersize=15)
# Zeichne Extremstellen als X
for one_inf in inflection_points:
plt.plot(one_inf, sp.N(p.subs(x, one_inf)), "rx", markersize=15)
# Zeichne eine horizontale Linie bei 0 von -3 bis 3
plt.hlines(0, -3, 3, "k")
# Schreibe das Polynom als Plot-Titel über die Figur
plt.title(p)
# Generiere die Legende
plt.legend(loc=0)
# Zeige den Plot
plt.show()
# Jetzt rufen wir das für eine andere Kurve auf
p = x**4 - 4
perform_curve_sketching(p, x, x_vals)
# Jetzt rufen wir das für eine andere Kurve auf
p = x**6 - 3*x**5 + 2*x**3 - 4*x + 1
perform_curve_sketching(p, x, x_vals)