- Startseite
- Allgemeine Informationen zur Lehrveranstaltung
- Einfaches Python Setup und Wichtige Informationen
- 0. Python Einführung und Checkup
- 1. Einführung und einfache Algorithmen
- 2. Differenzieren und Integrieren
- 3. Vektoren, Matrizen und Vektorisierung in Python
- 4. Datenanalyse bzw. Datenauswertung
- 5. Grundlagen der Optimierung und Gradient Descent
- 6. Stochastische Optimierung und Genetische Algorithmen
- 7. Monte-Carlo-Methoden – Simulation und Integration
- 8. Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk
- 9. Unsupervised Machine Learning: Clustering von Daten
- 10. Supervised Machine Learning: Grundlagen
- 11. Einführung in künstliche neuronale Netzwerke
Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.
8. Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk¶
Im vorangegangenen Notebook haben wir uns mit Monte-Carlo-Methoden im Allgemeinen beschäftigt. Am Ende der Einheit haben wir außerdem das Konzept der Monte-Carlo-Integration gestreift, und zwar mit der Berechnung einer Näherung der Zahl $\pi$ über zufällig verteilte Punkte auf dem Einheitsquadrat. Das ist jedoch nicht die typische Art und Weise, Monte-Carlo-Integration zu betreiben.
Obwohl man mit einer Integration die Fläche unter der Kurve einer Funktion berechnet, ist das komplett analoge Beispiel mit der Berechnung von $\pi$ unter der Kurve des Viertelkreises, der im Einheitsquadrat eingeschrieben ist, tatsächlich mehr ein anschauliches Beispiel für eine MC-Simulation. Die MC-Integration verwendet allerdings meist ein anderes Prinzip.
8.1 Das Integral als Erwartungswert über eine Zufallsvariable¶
Konkret haben wir in der vergangenen Einheit den Wert des folgenden Integrals simuliert: $$4\int_0^1 dx \sqrt{1-x^2}$$ Das Resultat war eine Näherung der Zahl $\pi$, eine Fehlerabschätzung inklusive (weil wir mehrere Samples verwendet haben. Muss man das Integral allerdings tatsächlich so umständlich berechnen (also viele Punkte auf die ganze Fläche werfen, dann bestimmen welche unter dem Funktionswert liegen und welche darüber, alles abzählen und das Verhältnis bilden) oder geht das einfacher?
Es geht tatsächlich einfacher. Der Trick ist, das Integral, das wir gerade aufgeschrieben hatten, als Erwartungswert einer Funktion zu interpretieren. Um das noch etwas besser zu sehen, schreiben wir das Integral nochmals auf, und zwar zunächst einmal so: $$\int_{x_{min}}^{x_{max}} dx h(x)$$ Wir haben hier noch nicht viel gemacht, außer die Integrationsgrenzen mit zwei Variablen zu benennen, die Funktion allgemein als $h$ zu bezeichnen und den (irrelevanten) Vorfaktor wegzulassen. Der nächste Schritt ist allerdings der wesentliche. Wir schreiben das gleiche Integral jetzt als: $$\int_{x_{min}}^{x_{max}} dx f(x) g(x)$$ Auch das ist keine Hexerei, denn wir haben einfach nur die Funktion $h$ als ein Produkt von zwei anderen Funktionen $f$ und $g$ geschrieben. Warum ist das jetzt so viel besser als vorher?
Die Antwort auf diese Frage ist, dass uns nun die Interpretation als Erwartungswert leichter fällt. Sagen wir, $f$ sei eine Funktion, von der wir den Erwartungswert berechnen. Und $g$ ist eine Wahrscheinlichkeitsverteilung, und zwar der Zufallsvariablen $x$, deren Werte zwischen ${x_{min}}$ und ${x_{max}}$ liegen. Dann definiert dieses Integral tatsächlich den Erwartungswert der Funktion $f$ über die $g$-verteilte Zufallsvariable $x$.
Alles schön und gut, aber wie veranstalten wir damit nun eine MC-Integration?
8.2. Näherung des Erwartungswerts durch Sampling¶
Wir nähern das Integral, also den Erwartungswert durch Sampling der Zufallsvariablen $x$. Konkret müssen wir dazu folgendes tun:
- Den eigentlichen Integranden in ein Produkt von zwei Funktionen $f$ und $g$ zerlegen
- Eine der beiden (in unserem Beispiel $g$) als Wahrscheinlichkeitsverteilung interpretieren (und verwenden können)
- Wir sampeln $N$ Werte $x_i$ für $x$, und zwar aus der Verteilung $g$
- Wir bestimmen die Summe $$\frac{1}{N} \sum_{i=1}^N f(x_i)$$
- Wir betreiben wieder Statistik mit mehreren Samples und bestimmen Mittelwerte und Standardabweichung
Soweit, so gut. Sehen wir uns jetzt nochmals das Integral an, das zum Wert von $\pi$ führt: $$4\int_0^1 dx \sqrt{1-x^2}$$ Hier kann man z.B. einfach $f(x)=\sqrt{1-x^2}$ und $g(x)=1$ (also gleichverteilte Zufallszahlen) nehmen. Somit ergibt sich für die Näherung des Integrals die Summe $$\frac{1}{N} \sum_{i=1}^N \sqrt{1-x_i^2}$$ mit gleichverteilten $x_i$.
Probieren wir das mal aus.
8.3 Näherungswert für $\pi$, revisited¶
%matplotlib inline
# zunächst die Imports für heute
import numpy as np
# die Halbnormalverteilung importieren wir aus SciPy
from scipy.stats import halfnorm
# Matplotlib wie gewohnt
import matplotlib.pyplot as plt
# Auch SymPy bekommt hier ein kurzes Gastspiel
import sympy as sp
# Und tqdm für den Fortschrittsbalken
from tqdm import tqdm
Zunächst lohnt es sich, der Übersichtlichkeit halber ein paar Schritte des Prozesses als Funktionen zu definieren. Die Schritte, die wir hier machen, sind:
- Die Funktion, um die es geht
- Die Summe (eigentlich der Mittelwert) als Näherung des Erwartungswertes
- Das Wiederholen des Aufrufs für mehrere Samples und die damit verbundene Statistik
Was wir hier nicht als Argument einer Funktion einbauen, ist die spezifische Wahrscheinlichkeitsverteilung, die wir verwenden wollen. Die Gleichverteilung wird stattdessen erstmal fix eingebaut.
# definiere Funktion für den Aufruf (NumPy-geeignet)
def pi_function(x):
# die Wurzelfunktion direkt zurückgeben
return 4 * np.sqrt(1 - x**2)
# definiere Funktion zur Berechnung der Näherungssumme
def approximate_by_average(the_function, x_values):
# gib die Summe der Funktionswerte an den gewünschten Stellen
# dividiert durch die Zahl der Punkte zurück
# das Average läuft dabei nur über die letzte Dimension des Arrays
return np.mean(the_function(x_values), axis=-1)
# definiere Funktion zum Berechnen und Auswerten mehrerer Samples
def evaluate_n_samples(the_call, the_function, n_samples=20, n_points=100):
# Rufe Samples auf
the_output = the_call(the_function, np.random.random(size=(n_samples, n_points)))
# Berechne Statistik
the_means = np.mean(the_output, axis=-1)
the_sigmas = np.std(the_output, axis=-1)
# gib Mittelwerte und Standardabweichungen zurück
return the_means, the_sigmas
Als nächstes können wir nun diese Funktionen zusammensetzen und damit eine Simulation bzw. Integration starten. Die Ergebnisse sehen wir uns in Abhängigkeit von der Anzahl der verwendeten Punkte pro Summe bzw. Erwartungswert an. Nachdem der Loop durchgelaufen ist, werden auch noch die Ergebnisse entsprechend ausgegeben.
# initialisiere Liste für Mittelwerte und Sigmas
mean_list = []
sigma_list = []
# definiere Liste für verschiedene Werte für N
n_list = [10, 100, 1000, 10000, 100000, 10000000]
# loop über diese Werte von N
for an_n in tqdm(n_list):
# rufe die Summe auf, mit entsprechendem Wert für N
means_sum, stds_sum = evaluate_n_samples(approximate_by_average, pi_function, n_samples=20, n_points=an_n)
# hänge Werte von mean und sigma an die Sammelliste an
mean_list.append(means_sum)
sigma_list.append(stds_sum)
# Ausgabe der Resultate während des Loops
print("Näherung für Pi mit", an_n, "Punkten:", means_sum, "+-", stds_sum)
print("Unterschied zu Pi:", means_sum - np.pi, "\n")
# gib die Listen aus
print("Mittelwerte:", mean_list)
print("Standardabweichungen:", sigma_list)
0%| | 0/6 [00:00<?, ?it/s]
Näherung für Pi mit 10 Punkten: 3.182888494049963 +- 0.2919599358096478 Unterschied zu Pi: 0.041295840460169764 Näherung für Pi mit 100 Punkten: 3.166754030813454 +- 0.09727596780359392 Unterschied zu Pi: 0.025161377223660963 Näherung für Pi mit 1000 Punkten: 3.131525116567528 +- 0.02789525859649153 Unterschied zu Pi: -0.01006753702226515 Näherung für Pi mit 10000 Punkten: 3.141978395587277 +- 0.011889041212797933 Unterschied zu Pi: 0.0003857419974839793 Näherung für Pi mit 100000 Punkten: 3.142505674710769 +- 0.0037917561127985026 Unterschied zu Pi: 0.0009130211209757988
100%|██████████| 6/6 [00:05<00:00, 1.07it/s]
Näherung für Pi mit 10000000 Punkten: 3.14155191374144 +- 0.00026076443789357375 Unterschied zu Pi: -4.073984835306632e-05 Mittelwerte: [3.182888494049963, 3.166754030813454, 3.131525116567528, 3.141978395587277, 3.142505674710769, 3.14155191374144] Standardabweichungen: [0.2919599358096478, 0.09727596780359392, 0.02789525859649153, 0.011889041212797933, 0.0037917561127985026, 0.00026076443789357375]
8.4 Verwendung der Wahrscheinlichkeitsverteilung¶
Bisher haben wir noch nicht wirklich Gebrauch von der Möglichkeit gemacht, die Wahrscheinlichkeitsverteilung eigentlich ziemlich beliebig aus dem Integral zu separieren. Aber auch dafür wollen wir uns jetzt ein Beispiel ansehen. Dabei geht es um das Integral $$\int_0^\infty dx\; x^3 e^{-x^2}$$
Um es zu mit MC-Integration zu berechnen, nehmen wir es wie folgt auseinander: $f(x)=x^3$ und $g(x)=e^{-x^2}$. Dabei stellen wir fest, dass $g$ noch nicht ganz einer Wahrscheinlichkeitsverteilung entspricht. Genauer gesagt, hat eine Normalverteilung mit Mittelwert $0$ die folgende Form $$\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{x^2}{2\sigma^2}}$$ Ein anderes Problem ist, dass wir nur eine Seite der Normalverteilung brauchen, weil das Integral von $0$ bis $\infty$ reicht. Wir nehmen also stattdessen die sogenannte Halbnormalverteilung der Form $$\frac{\sqrt{2}}{\sigma\sqrt{\pi}} e^{-\frac{x^2}{2\sigma^2}}$$
Damit das zusammenpasst, müssen wir also $\sigma=1/\sqrt{2}$ setzen, und es ergibt sich die Verteilung $$\frac{2}{\sqrt{\pi}} e^{-x^2}$$ Damit haben wir also als korrekte Zerlegung $f(x)=\frac{\sqrt{\pi}}{2} x^3$ und $g(x)=\frac{2}{\sqrt{\pi}} e^{-x^2}$ gefunden. Und damit ergibt sich für die Näherung des Integrals die Summe $$\frac{1}{N} \sum_{i=1}^N \sqrt{\pi}x_i^3 / 2$$ mit halbnormalverteilten $x_i$.
Zur Kontrolle sehen wir uns einmal das Integral an, wie SymPy es berechnet:
# Erzeuge SymPy-Symbol (Variable) x
x = sp.Symbol("x")
# Definiere die Funktion
function_2 = x**3 * sp.exp(-x**2)
# Berechne den numerischen Wert des Integrals der Funktion von 0 bis undendlich
sp.N(sp.integrate(function_2, (x, 0, sp.oo)))
Als nächstes machen wir nun die numerische Abschätzung via MC-Integration. Dafür habe ich von oben nochmal die entsprechenden Zellen kopiert und die Funktion angepasst, sowie die Wahrscheinlichkeitsverteilung ausgetauscht.
# definiere Funktion für den Aufruf (NumPy-geeignet)
def x3_function(x):
# die Funktion direkt zurückgeben
return np.sqrt(np.pi) * x**3 / 2
# definiere Funktion zum Berechnen und Auswerten mehrerer Samples
def evaluate_n_samples_halfnormal(the_call, the_function, n_samples=20, n_points=100):
# Rufe Samples auf, der Zufallszahlenbefehl ist hier (SciPy) etwas anders
the_output = the_call(the_function, halfnorm.rvs(size=(n_samples, n_points), scale=1/np.sqrt(2)))
# Berechne Statistik
the_means = np.mean(the_output, axis=-1)
the_sigmas = np.std(the_output, axis=-1)
# gib Mittelwerte und Standardabweichungen zurück
return the_means, the_sigmas
# initialisiere Liste für Mittelwerte und Sigmas
mean_list = []
sigma_list = []
# definiere Liste für verschiedene Werte für N
n_list = [10, 100, 1000, 10000, 100000, 1000000, 10000000]
# loop über diese Werte von N
for an_n in tqdm(n_list):
# rufe die Summe auf, mit entsprechendem Wert für N
means_sum, stds_sum = evaluate_n_samples_halfnormal(approximate_by_average, x3_function, n_samples=20, n_points=an_n)
# hänge Werte von mean und sigma an die Sammelliste an
mean_list.append(means_sum)
sigma_list.append(stds_sum)
# Ausgabe der Resultate während des Loops
print("Näherung für 0.5 mit", an_n, "Punkten:", means_sum, "+-", stds_sum)
print("Unterschied zu 0.5:", means_sum - 0.5, "\n")
# gib die Listen aus
print("Mittelwerte:", mean_list)
print("Standardabweichungen:", sigma_list)
0%| | 0/7 [00:00<?, ?it/s]
Näherung für 0.5 mit 10 Punkten: 0.4563206877909283 +- 0.21645612167170966 Unterschied zu 0.5: -0.043679312209071675 Näherung für 0.5 mit 100 Punkten: 0.46435914787955357 +- 0.10384478854423947 Unterschied zu 0.5: -0.03564085212044643 Näherung für 0.5 mit 1000 Punkten: 0.5159776416138581 +- 0.04297139507303872 Unterschied zu 0.5: 0.015977641613858062 Näherung für 0.5 mit 10000 Punkten: 0.5033704725040146 +- 0.010712594688818371 Unterschied zu 0.5: 0.0033704725040145656
71%|███████▏ | 5/7 [00:00<00:00, 41.63it/s]
Näherung für 0.5 mit 100000 Punkten: 0.49952385313255626 +- 0.004849344454136434 Unterschied zu 0.5: -0.0004761468674437386 Näherung für 0.5 mit 1000000 Punkten: 0.5001181851240026 +- 0.001057633638660564 Unterschied zu 0.5: 0.00011818512400263437
100%|██████████| 7/7 [00:12<00:00, 1.72s/it]
Näherung für 0.5 mit 10000000 Punkten: 0.49991003607040296 +- 0.0004039890985762624 Unterschied zu 0.5: -8.99639295970367e-05 Mittelwerte: [0.4563206877909283, 0.46435914787955357, 0.5159776416138581, 0.5033704725040146, 0.49952385313255626, 0.5001181851240026, 0.49991003607040296] Standardabweichungen: [0.21645612167170966, 0.10384478854423947, 0.04297139507303872, 0.010712594688818371, 0.004849344454136434, 0.001057633638660564, 0.0004039890985762624]
# Hier noch eine grafische Darstellung
fig = plt.figure()
# Plotte Mittelwerte mit Fehlerbalken
plt.errorbar(n_list, mean_list, yerr=sigma_list, xerr=None,
fmt="o-", markersize=10, color="b", ecolor="red", capsize=10, capthick=2)
# Schalte x-Achse (N) auf logarithmische Skalierung
plt.xscale("log")
# Achsenbeschriftungen
plt.xlabel(r"$N$")
plt.ylabel("Wert des Integrals")
# Grafik anzeigen
plt.show()
Mit dieser Technik lassen sich im Prinzip beliebige Integrale numerisch nähern. Was wir hier nicht gemacht haben, was aber diesbezüglich wichtig ist: Die Methode funktioniert nicht nur genauso gut in mehr als einer Dimension, sie ist sogar besonders effizient, je höher die Anzahl der Dimensionen wird. Dazu noch ein Detail, das Sie sich gut merken können (auch, weil wir es in der vergangenen Einheit explizit gezeigt haben):
Der Fehler bei der Monte-Carlo-Integration skaliert wie der Kehrwert der Wurzel aus $N$, der Anzahl der verwendeten Punkte bzw. der Sample-Größe. Dieser Wert hängt nicht von der Dimension des Integrals ab, während das für andere numerische Integrationsmethoden sehr wohl der Fall ist (z.B. für Gauss-Quadratur-Verfahren muss man eine Anzahl Integrationspunkte in jeder Dimension festlegen). Wenn Sie sich also nur eine Eigenschaft bei Monte-Carlo-Methoden merken, dann merken Sie sich das:
Der Fehler skaliert wie $\frac{1}{\sqrt{N}}$.
8.5 Komplexeres Beispiel für Monte-Carlo-Simulation: Random Walk¶
Nachdem Sie nun mit der spezifischen Technik der MC-Integration vertraut sind, wenden wir uns wieder der allgemeinen Simulation zu. Insbesondere sehen wir uns ein Problem an, dem Sie vielleicht auch einmal im echten Leben begegnen werden: Dem Random Walk.
Damit ist folgendes gemeint: Wir stellen uns folgende Situation bzw. folgendes System vor:
- Ein Mensch/Hund/Roboter, nennen wir ihn “agent”, kann Schritte ausführen
- Die Schritte können in der Größe fixiert sein, oder durch eine Wahrscheinlichkeitsverteilung bestimmt werden
- Die Richtung eines Schrittes kann ebenfalls eingeschränkt sein (z.B. entlang der Koordinatenachsen auf einem Gitter) oder in beliebiger Richtung ausgeführt werden können
- Die Richtung wird für jeden Schritt zufällig über eine Wahrscheinlichkeitsverteilung gewählt
- Jeder Schritt wird von der Position ausgeführt, an der der vorige Schritt geendet hat
- Die Bewegung, die so entsteht, ist ein zusammenhängender Weg
- Simuliert man viele solcher Wege, dann erhält man verschiedene Informationen, wie immer über die statistische Auswertung der Ergebnisse
Somit haben wir das Grundgerüst, das eigentlich sehr übersichtlich und ziemlich geradlinig ist. Deshalb wollen wir uns das gleich einmal konkret ansehen.
# definiere Funktion für einen Schritt in 2D
def step(size=1):
# wir machen das wieder vectorizable, sodass wir mehrere
# Walks auf einmal laufen lassen können
# hier zuerst die Richtung, beliebig aus 2 Pi ausgewählt
directions = 2 * np.pi * np.random.random(size=size)
# dann noch die Schrittgröße, die wir hier einmal auf 1 fixieren
strides = np.ones(size)
# daraus berechnen wir die Unterschiede in x und y Richtung
delta_x = strides * np.cos(directions)
delta_y = strides * np.sin(directions)
# das Resultat hat also Dimension 2 x size
return delta_x, delta_y
Nachdem die Funktion für einen Schritt in mehreren Walks definiert ist, werden wir nun eine Runde von Walks laufen lassen. Dafür brauchen wir jeweils eine Anzahl von Schritten und Walks, und dann einen Loop, bei dem die Schritte ausgeführt und die Positionen mitgeschrieben werden.
# definiere Anzahl der Schritte in einem Walk
n_steps = 1000 # erhöhe auch auf 100, 1000
# definiere Anzahl der Walks die gleichzeitig laufen
n_simultaneous_walks = 1000 # erhöhe auch auf 100, 1000
# initialisiere Positionen für alle Walks am Anfang:
# 2 Koordinaten pro Walk, 1. Zeile im Positionsarray
positions = np.zeros((1, n_simultaneous_walks, 2))
# Loop über Schritte
for ind_steps in tqdm(range(n_steps)):
# addiere die transponierten Deltas zur letzten Position in der Liste
# und berechne dadurch die neuen Positionen in allen Walks
# das Transponieren bringt die xy Werte für alle Walks an die richtige Stelle
new_positions = positions[-1] + np.transpose(step(size=n_simultaneous_walks))
# und hänge die neue Position an die Positionsliste an
# dafür brauchen die neuen Positionen eine Dimension mehr, sonst passt das Array
# nicht zu den positions
positions = np.append(positions, np.reshape(new_positions, (1, -1, 2)), axis=0)
# jetzt machen wir gleich noch eine grafische Darstellung
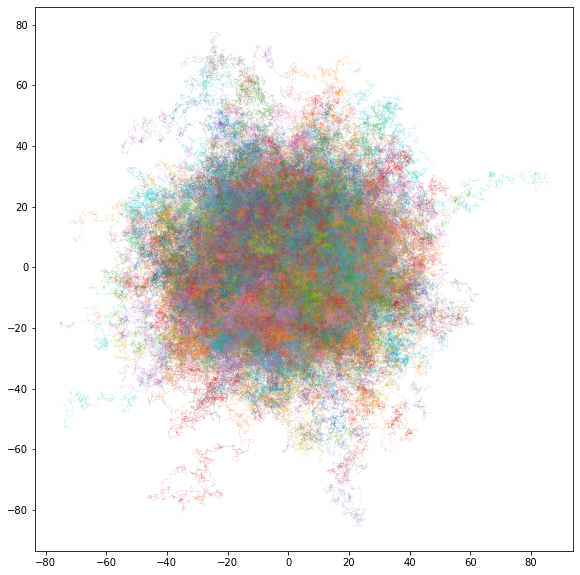
fig = plt.figure(figsize=(10,10))
# setze Ascpect-Ratio des Plots auf 1, damit die Form der Walks stimmt
ax = plt.gca()
ax.set_aspect(1)
# zum leichteren Plotten bringen wir die Dimensionen im fertigen Array
# der Positionen in eine andere Reihenfolge:
# vorher: Schritte x Walks x xy
# nachher: Walks x xy x Schritte
positions = np.transpose(positions, (1, 2, 0))
# durch das Transponieren bzw. Permutieren kann man nun einfach einen
# Loop über den 0. Index laufen lassen
for ind_walks in tqdm(range(n_simultaneous_walks)):
# die xy Koordinaten kann man dann einfach übergeben
# und der letzte Index ist dann die Abfolge der Schritte für die Linie
plt.plot(*positions[ind_walks], linewidth=.1)
# hier zahlt es sich aus, die Figur auch abzuspeichern, um sie besser
# ansehen zu können. Zwei Formate sind interessant:
# erstens png als typisches Bildformat, möglich wäre auch jpg
# plt.savefig("random_walk.png", dpi=1200)
# zweitens pdf als Vektorformat (d.h. die Auflösung bei der
# Darstellung wird an die Bildgröße angepasst)
plt.savefig("random_walk.pdf")
# Und Grafik anzeigen
plt.show()
100%|██████████| 1000/1000 [00:00<00:00, 2002.51it/s] 100%|██████████| 1000/1000 [00:00<00:00, 3738.63it/s]
Nachdem wir jetzt die Daten erzeugt und auch bereits visualisiert haben, wollen wir sie noch etwas auswerten. Dafür können wir einfach das NumPy-Array mit den Positionen verwenden und bestimmte Dinge berechnen (und dann ebenfalls grafisch darstellen). Interessant sind z.B.
- Mittlere Entfernung vom Ursprung in Abhängigkeit von der Anzahl der Schritte
- Maximale Entfernung vom Ursprung in Abhängigkeit von der Anzahl der Schritte
- Richtung am letzten Punkt im Walk
Sehen wir uns das alles einfach der Reihe nach an:
# zur Erinnerung: Die Dimensionen in positions sind: Walks x xy x Schritte
# berechne zunächst die Distanzen über den Satz von Pythagoras
distances = np.sqrt(np.sum(positions**2, axis=1))
# berechne nun die Durchschnittsdistanzen für alle Walks
average_distances = np.mean(distances, axis=1)
# Ausgabe der Statistik
print("Mittlere Durchschnittsdistanz:", np.round(np.mean(average_distances), 2), "+-", np.round(np.std(average_distances), 2))
# Erzeuge neue Grafik
fig = plt.figure(figsize=(10,8))
# Diesmal nehmen wir verschiedene Möglichkeiten zur Visualisierung
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 1
ax1 = plt.subplot(2,2,1)
# Erste Möglichkeit: Plotte Distanz als Funktion des Walks
ax1.plot(average_distances)
ax1.set_xlabel("Walks")
ax1.set_ylabel("Durchschnittsdistanz vom Ursprung")
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 2
ax2 = plt.subplot(2,2,2)
# Zweite Möglichkeit: Plotte Distanz als Funktion des Walks,
# aber geordnet nach aufsteigenden Werten
ax2.plot(np.sort(average_distances))
ax2.set_xlabel("Walks, geordnet nach Werten")
ax2.set_ylabel("Durchschnittsdistanz vom Ursprung")
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 3
ax3 = plt.subplot(2,2,3)
# Dritte Möglichkeit: Plotte Distanzen in einem Histogramm
ax3.hist(average_distances)
ax3.set_xlabel("Durchschnittsdistanz vom Ursprung")
ax3.set_ylabel("Walks")
plt.show()
Mittlere Durchschnittsdistanz: 18.7 +- 7.62
# berechne nun die maximalen Distanzen für alle Walks
max_distances = np.max(distances, axis=1)
# Ausgabe der Statistik
print("Mittlere Maximaldistanz:", np.round(np.mean(max_distances), 2), "+-", np.round(np.std(max_distances), 2))
# Erzeuge neue Grafik
fig = plt.figure(figsize=(10,8))
# Wir nehmen wieder verschiedene Möglichkeiten zur Visualisierung
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 1
ax1 = plt.subplot(2,2,1)
# Erste Möglichkeit: Plotte Distanz als Funktion des Walks
ax1.plot(max_distances)
ax1.set_xlabel("Walks")
ax1.set_ylabel("Maximaldistanz vom Ursprung")
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 2
ax2 = plt.subplot(2,2,2)
# Zweite Möglichkeit: Plotte Distanz als Funktion des Walks,
# aber geordnet nach aufsteigenden Werten
ax2.plot(np.sort(max_distances))
ax2.set_xlabel("Walks, geordnet nach Werten")
ax2.set_ylabel("Maximaldistanz vom Ursprung")
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 3
ax3 = plt.subplot(2,2,3)
# Dritte Möglichkeit: Plotte Distanzen in einem Histogramm
ax3.hist(max_distances)
ax3.set_xlabel("Maximaldistanz vom Ursprung")
ax3.set_ylabel("Walks")
plt.show()
Mittlere Maximaldistanz: 36.82 +- 12.72
# Jetzt kommt noch die Visualisierung der Richungen
# zur Erinnerung: Die Dimensionen in positions sind: Walks x xy x Schritte
# berechne zunächst die Richtungen über den Arcustangens
final_positions = positions[:, :, -1]
directions = np.arctan(final_positions[:, 1]/final_positions[:, 0])
# berechne nun die Durchschnittsrichtung für alle Walks
average_direction = np.mean(directions)
# Ausgabe der Statistik
print("Mittlere Richtung:", np.round(average_direction, 2), "+-", np.round(np.std(directions), 2))
# Erzeuge neue Grafik
fig = plt.figure(figsize=(10,8))
# Diesmal nehmen wir vier verschiedene Möglichkeiten zur Visualisierung
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 1
ax1 = plt.subplot(2,2,1)
# Erste Möglichkeit: Plotte finale Positionen aller Walks
ax1.scatter(*np.transpose(final_positions), s=.3)
ax1.set_xlabel("x")
ax1.set_ylabel("y")
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 2
ax2 = plt.subplot(2,2,2)
# Zweite Möglichkeit: Plotte Averages von finalen x und y mit Fehlerbalken
ax2.errorbar(*np.mean(final_positions, axis=0),
xerr=np.std(final_positions[:, 0]),
yerr=np.std(final_positions[:, 1]),
elinewidth=1.5, capsize=15,
fmt='o', markersize=15)
ax2.set_xlabel("Walks")
ax2.set_ylabel("Richtung am Ende des Walks")
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 3
ax3 = plt.subplot(2,2,3)
# Dritte Möglichkeit: Plotte Richtungen als Funktion des Walks
ax3.plot(directions)
ax3.set_xlabel("Walks")
ax3.set_ylabel("Richtung am Ende des Walks")
# Erzeuge einen Subplot in einem 2x2 Raster an der Stelle 4
ax4 = plt.subplot(2,2,4)
# Vierte Möglichkeit: Plotte Richtungen als Funktion des Walks,
# geordnet nach aufsteigenden Werten
ax4.plot(np.sort(directions))
ax4.set_xlabel("Walks, geordnet nach Werten")
ax4.set_ylabel("Richtung am Ende des Walks")
plt.show()
Mittlere Richtung: -0.01 +- 0.87
8.6 Übungsaufgabe: Experimentieren mit dem Random Walk¶
Für die Untersuchungen von Random Walks gibt es viele Möglichkeiten. Experimentieren Sie nun mit diesem Problem. Kopieren Sie den Code von oben und testen Sie je nach Zeit und Möglichkeit (und unter anderem, je nachdem, was Sie sonst noch alles verändern möchten) folgende Änderungen/Szenarien:
- Ändern Sie die Schrittweite auf eine andere Konstante. Was passiert?
- Wählen Sie die Schrittweite zufällig aus einer Wahrscheinlichkeitsverteilung Ihrer Wahl. Was passiert?
- Verpassen Sie dem Random Walk eine “Schlagseite” (“Biased Random Walk”), d.h. machen Sie z.B. die Schrittweite von der Richtung abhängig. Was passiert?
- Schränken Sie die Richtung auf ein Gitter ein (also die Richtung auf z.B. die 4 Winkel 0, 90, 180, 270 Grad). Was passiert?
- Erhöhen Sie die Anzahl der Schritte und beobachten Sie die Werte für mittlere und maximale Distanz vom Ursprung. Können Sie eine bestimmte Abhängigkeit dieser Größen von der Anzahl der Schritte feststellen?