Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.

Monte-Carlo Methoden – Simulation und Integration

7 Monte-Carlo Methoden – Simulation und Integration¶

In diesem Notebook beschäftigen wir uns mit den sogenannten Monte-Carlo Methoden. Im wesentlichen handelt es sich dabei um einen Satz von Methoden, die verschiedene Situationen mit Hilfe von (Pseudo-)Zufallszahlen simulieren oder verschiedene Größen auf diese Art berechnen helfen.

Recht bekannt ist die Monte-Carlo Integration, mit der wir uns im zweiten Teil dieser Einheit beschäftigen werden. Zunächst sollen Sie allerdings eine allgemeinere Einführung in die Anwendung von Monte-Carlo Methoden bekommen, denn die Monte-Carlo Integration ist eher als Spezialfall anzusehen.

7.1 Allgemeine Strategie einer Monte-Carlo Simulation¶

Die allgemeine Strategie einer MC-Simulation ist eigentlich recht simpel und geradlinig: Man nehme eine interessante Situation/Fragestellung, deren Regeln man kennt, setze diese in einem Computerprogramm um, lasse dieses Programm einige (viele viele) Male laufen, und werte die Ergebnisse statistisch aus.

Was das Wort “statistisch” hier soll, dazu kommen wir gleich noch. Aber grundsätzlich würde es für eine super-brutale erste Näherung auch genügen, das Programm nur einmal laufen zu lassen. Dann hätte man ein Ergebnis, mit dem man de facto auch bereits einen Teil der Antwort auf die Fragestellung bekommt, aber eben nur einen Teil.

Und zwar deshalb, weil in einer MC-Simulation der Zufall (bzw. Pseudozufallszahlen) eine große Rolle spielt. Somit ist das eine Ergebnis, das man bekommen hat, eben auch nur ein möglicher Ausgang der Situation, mit der man sich befasst. Was sonst noch alles passieren kann, das kommt erst ans Licht, wenn man das Programm eben sehr oft laufen lässt. Zum besseren Verständnis einer ordentlichen Auswertung einer MC-Simulation kommen wir kurz zu ein paar Begriffen zurück, die uns bereits begegnet sind:

7.2 Samples, Sample-Means¶

Wir haben bereits in der vergangenen Einheit (bei der Stochastischen Optimierung) über Sampling gesprochen. Damals ging es in erster Linie darum, dass ein Sample ein Satz von Zufallszahlen ist, mit dem man irgendeine Berechnung anstellt. Im Kontext der MC-Simulation ist ein Sample jedoch noch etwas mehr, nämlich ein Teil der Simulation. Die gesamte Simulation besteht aus mehreren Samples, die kombiniert werden, um die statistische Auswertung klar zu machen. Wieso, dazu gleich mehr im folgenden Abschnitt.

Zunächst aber noch zum Mittelwert einer Größe in einem Sample. Wenn wir z.B. einen Würfel werfen (siehe auch weiter unten), dann beträgt der Mittelwert der Augen, gemessen über ein Sample, die Anzahl der im Sample geworfenen Augen durch die Anzahl der Würfe. Das ist dann das Sample-Mean. Analog kann man für ein Sample auch verschiedene andere Eigenschaften von Variablen bestimmen, wie z.B. die Standardabweichung, etc.

Das ist schon ein guter Anfang, doch es geht noch besser.

7.3 Der Zentrale Grenzwertsatz und Mean of Sample-Means¶

Der zentrale Grenzwertsatz (auf Englisch “Central-Limit Theorem”) soll uns hier nicht sehr grundlegend beschäftigen, sondern eher als Erklärung und Motivation dafür dienen, einen Satz von Samples für die Auswertung einer MC-Simulation zu verwenden.

Genauer gesagt nehmen wir die Mittelwerte einer Größe aus mehreren Samples und mitteln diese nochmals zu einem Sample-Mean. Wieso? Der Zentrale Grenzwertsatz besagt, dass für mehrere Zufallsvariablen, die der gleichen Verteilung folgen, die Verteilung der Sample-Means normalverteilt ist. Das bedeutet:

Nimmt man ein Sample und berechnet damit einen Mittelwert, dann hat man zwar einen Anhaltspunkt für den Mittelwert der tatsächlichen zugrundeliegenden Verteilung, aber nicht mehr.
Nimmt man die Sample-Means und berechnet deren Mean und Standardabweichung (das darf man, denn die Verteilung ist ja eine Normalverteilung), dann hat man sowohl eine bessere Näherung für den tatsächlichen Mittelwert, als auch gleichzeitig eine Abschätzung für den statistischen Fehler in der Bestimmung dieses Mittelwerts.
Wenn man nun die Anzahl der Elemente eines Samples erhöht (also die Samplegröße), dann bekommt man grundsätzlich genauere Werte für den Mittelwert.
Wenn man allerdings mehrere Samples verwendet, dann bekommt man eine bessere Einschätzung des Fehlers im Mittelwert.

Wir werden damit gleich experimentieren, damit Sie sehen, was gemeint ist.

7.4 Beispiel: Böse Eins¶

Als einfaches Beispiel wollen wir uns ein einfaches Würfelspiel ansehen, das mit nur einem normalen Würfel (D6) gespielt wird: Böse Eins. Die Regeln dafür, hier von SpielWiki übernommen, lauten:

Die Spieler würfeln der Reihe nach mit einem Würfel. Jeder Spieler darf fünfmal würfeln. Die Augen aus den einzelnen Würfen werden notiert. Wirft man jedoch eine Eins, werden die Augen der jeweiligen Runde ungültig. Sieger ist, wer als erster 100 Punkte hat.

Um dieses Spiel zu simulieren, lassen wir mehrere Samples von Durchläufen für das Spiel von einem Programm durchrechnen. Für die Analyse wählen wir Größen aus, die uns geeignet erscheinen, das zu erfahren, was wir wissen wollen oder was interessant scheint, z.B.:

Was ist die durchschnittliche Punktzahl pro Spieler pro Runde?
Nach wie vielen Runden ist ein Spiel durchschnittlich zu Ende?

Diese Größen zeichnen wir dann während der Simulation zu geeigneten Zeitpunkten auf, um am Ende dann die entsprechenden Statistiken anzufertigen. Die statistische Auswertung wird wieder zunächst über die Runs, dann innerhalb der Samples, und schließlich über die Samples gemacht, sodass wir fundierte Informationen bekommen.

Legen wir also los.

In [1]:

%matplotlib inline

# Die Imports für heute
import numpy as np

import matplotlib.pyplot as plt

from tqdm import tqdm

In [2]:

# Definiere Würfe für den D6-Würfel
def roll_d6(size=None):
    
    # wähle aus den 6 Würfelseiten aus
    return np.random.choice(np.arange(1,7,1), size=size, replace=True)

# ein paar Würfe
roll_d6(size=(5))

Out[2]:

array([3, 1, 6, 2, 4])

In [3]:

# Definiere eine Runde für Böse 1
def boese_1_round(n_players=3, verbose=False):
    
    # 5 Würfe für jeden Spieler
    rolls = roll_d6(size=(n_players, 5))
    if verbose: print("Augen:\n", rolls)
    
    # finde Einsen in den Würfen
    evil_ones = np.where(rolls == 1, np.ones((n_players, 5)), np.zeros((n_players, 5)))
    if verbose: print("Positionen der Einsen:\n", evil_ones)
    
    # summiere die Augen auf, egal ob Einsen dabei sind oder nicht
    sums_of_rolls = np.sum(rolls, axis=1)
    if verbose: print("Wurfsummen:\n", sums_of_rolls)
    
    # Berechne die Punkte für jeden Spieler. Jene Spieler mit 1en erhalten 0 Punkte für die Runde
    points = np.where(np.sum(evil_ones, axis=1) == 0, sums_of_rolls, np.zeros(n_players))
    if verbose: print("Punkte:\n", points)
   
    return points

In [4]:

# teste diese Funktion
boese_1_round(n_players=3, verbose=True)

Augen:
 [[3 6 3 6 1]
 [6 1 4 4 6]
 [6 1 2 2 1]]
Positionen der Einsen:
 [[0. 0. 0. 0. 1.]
 [0. 1. 0. 0. 0.]
 [0. 1. 0. 0. 1.]]
Wurfsummen:
 [19 21 12]
Punkte:
 [0. 0. 0.]

Out[4]:

array([0., 0., 0.])

In [5]:

# nun setzen wir die Simulation des Spiels auf:

# Anzahl der Samples
n_samples = 200

# Samplegröße
n_games = 1000

# Anzahl der SpielerInnen
n_players = 3

# initialisiere Sammellisten für Sample-Means
sample_means_rounds = []
sample_means_avg_points = []

# Loop über Samples
for ind_samples in tqdm(range(n_samples)):
    
    # initialisiere Liste der Rundenzahl zum Sieg
    rounds_list = []
    
    # initialisiere Liste der Durchschnittspunkte pro Runde
    avg_points_per_round_list = []
    
    # Loop über Spiele
    for ind_games in range(n_games):
        
        # initialisiere das Punktemaximum
        max_points = 0.
        
        # initialisiere Zähler-Array für SpielerInnen
        points_array = np.zeros(n_players)
        
        # initialisiere Rundenzähler
        ind_rounds = 0
        
        # while-Loop über die Runden
        while max_points < 100:
            
            # erhöhe Rundenzähler
            ind_rounds += 1
            
            # Erzeuge Punkte für SpielerInnen
            new_points = boese_1_round(n_players=n_players, verbose=False)
            
            # hänge die Rundendurchschnittspunkte an die Sammelliste an
            avg_points_per_round_list.append(np.mean(new_points))
            
            # addiere neue Punkte zu den bisherigen
            points_array += new_points
            
            # berechne derzeitige Höchstpunktezahl
            max_points = np.max(points_array)
            
            # print("Derzeitiges Maximum:", max_points)
         
        # hänge Rundenzahl zum Sieg an Liste an
        rounds_list.append(ind_rounds)
        
    # berechne Means im Sample und hänge sie an Sammelliste über Samples an
    sample_means_rounds.append(np.mean(rounds_list))
    
    sample_means_avg_points.append(np.mean(avg_points_per_round_list))
    

100%|██████████| 200/200 [01:23<00:00,  2.39it/s]

In [6]:

# werte Sample-Means aus, für Runden
msm_rounds = np.round(np.mean(sample_means_rounds), 2)
ssm_rounds = np.round(np.std(sample_means_rounds), 2)
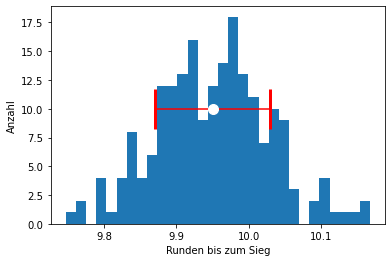
print("Durchschnitt Runden bis zum Sieg:", msm_rounds, "+-", ssm_rounds)
    
# und für Durchschnittspunkte
msm_points = np.round(np.mean(sample_means_avg_points), 2)
ssm_points = np.round(np.std(sample_means_avg_points), 2)
print("Durchschnitt Punkte pro Runde:", msm_points, "+-", ssm_points)
    
    

Durchschnitt Runden bis zum Sieg: 9.95 +- 0.08
Durchschnitt Punkte pro Runde: 8.04 +- 0.06

In [7]:

# und stelle sie grafisch dar
fig = plt.figure()

plt.hist(sample_means_rounds, bins=30)
plt.errorbar(msm_rounds, 10, yerr=None, xerr=ssm_rounds, 
             fmt="o", markersize=10, color="white", ecolor="red", capsize=20, capthick=3)

plt.xlabel("Runden bis zum Sieg")
plt.ylabel("Anzahl")

plt.show()

In [8]:

fig = plt.figure()

plt.hist(sample_means_avg_points, bins=30)
plt.errorbar(msm_points, 10, yerr=None, xerr=ssm_points, 
             fmt="o", markersize=10, color="white", ecolor="red", capsize=20, capthick=3)


plt.xlabel("Durchschnittspunkte pro Runde")
plt.ylabel("Anzahl")

plt.show()

Monte-Carlo-Methoden - Simulation und Integration 3

7.5 Monte-Carlo-Integration¶

An dieser Stelle möchte ich kurz auf die Monte-Carlo-Integration zu sprechen kommen. Diese ist im wesentlichen auch nichts anderes als eine MC-Simulation, nämlich eine “Simulation eines Integrals”. Das Prinzip kann man recht einfach mit der Berechnung der Zahl Pi demonstrieren, die “durchgeführt” wird, in dem man virtuelle Pfeile auf ein Dartboard wirft, genauer gesagt, auf einen Kreis, der einem Quadrat eingeschrieben ist. Sehen wir uns das gleich mal an.

Wir simulieren hier also folgenden Prozess:

Jemand hat $N$ Pfeile (Punkte)
Er verteilt diese zufällig auf einem Quadrat mit Seitenlänge $1$
Diesem Quadrat ist ein Viertelkreis (macht die Sache einfacher) eingeschrieben
Nachdem die Punkte verteilt sind, wird unterschieden und abgezählt:
- Wie viele Punkte liegen im Viertelkreis und
- wie viele Punkte liegen außerhalb des Viertelkreises?
Das Verhältnis von Punkte im Viertelkreis zu Gesamtpunkte ist eine Näherung des Verhältnisses der Flächeninhalte des Viertelkreises ($1^2 \pi / 4$) zu jenem des Quadrats ($1^2=1$), also für die Zahl $\pi / 4$.
Wenn man das statistische Verhältnis aus der Simulation also mit 4 multipliziert, erhält man eine Näherung für die Zahl $\pi$.

Und los geht’s:

In [9]:

# definiere Funktion, um zu prüfen, ob Paare von x und y im Einheitskreis liegen
def check_in_unit_circle(x, y):
    
    # bestimme Länge von x, d.h. Anzahl der Punkte
    n_points = len(x)
    
    # das funktioniert auch für numpy-Arrays
    return np.where(x**2 + y**2 <= np.ones(n_points), np.ones(n_points), np.zeros(n_points))

# definiere Funktion zum Erzeugen und Mitteln von Werten
def simulate_value_of_pi(n_samples = 20, # Anzahl der Samples
                         n_points = 100  # Samplesize = Anzahl der Punkte
                        ):

    # initialisiere Sammelliste für Sample-Means
    sample_means_ratios = []

    # Loop über Samples
    for ind_samples in tqdm(range(n_samples)):

        # initialisiere Punkte mit x und y Koordinaten
        points_array = np.random.random(size=(2, n_points))

        # checke, welche Punkte im Einheits-(Viertel-)Kreis sind
        hits_array = check_in_unit_circle(*points_array)  # kurz für (points_array[0], points_array[1])

        # berechne den Näherungswert für Pi
        inside_ratio_times_4 = 4 * np.sum(hits_array)/n_points

        # berechne Means im Sample und hänge sie an Sammelliste über Samples an
        sample_means_ratios.append(inside_ratio_times_4)
        
    # werte Sample-Means aus, für Pi-Näherungen, und gib sie mit dem Array als Ergebnis zurück
    return sample_means_ratios, np.mean(sample_means_ratios), np.std(sample_means_ratios)

In [10]:

# Rufe die Simulation auf
sample_means_ratios, msm_ratios, ssm_ratios = simulate_value_of_pi(n_samples = 200, n_points = 1000)

print("Näherung für Pi:", msm_ratios, "+-", ssm_ratios)

print("Unterschied zu Pi:", msm_ratios - np.pi)

100%|██████████| 200/200 [00:00<00:00, 26305.65it/s]

Näherung für Pi: 3.139 +- 0.05055175565695027
Unterschied zu Pi: -0.0025926535897933256

In [11]:

# und stelle sie grafisch dar
fig = plt.figure()

plt.hist(sample_means_ratios, bins=30)
plt.errorbar(msm_ratios, 10, yerr=None, xerr=ssm_ratios, 
             fmt="o", markersize=10, color="white", ecolor="red", capsize=20, capthick=3)

plt.xlabel("Runden bis zum Sieg")
plt.ylabel("Anzahl")

plt.show()

In [12]:

# Setze Anzahl der Punkte für den Plot neu
n_points = 1000   # erhöhe das auch auf 10000 und 100000

# mache ein Sample mit Farben und stelle es grafisch dar
points_array = np.random.random(size=(2, n_points))

# checke, welche Punkte im Einheits-(Viertel-)Kreis sind
hits_array = check_in_unit_circle(*points_array)

# mache farb-Array
# Vektor mit lauter "r"
red_array = np.chararray((n_points))
red_array[:] = "r"
red_array = np.array(red_array.astype(str))

# Vektor mit lauter "b"
blue_array = np.chararray((n_points))
blue_array[:] = "b"
blue_array = np.array(blue_array.astype(str))

# Farbarray, das zwei Farben hat, je nach drin oder draußen
color_array = np.where(hits_array, red_array, blue_array)

# nun plotten wir das
fig = plt.figure()

# setze Ascpect-Ratio des Plots auf 1
ax = plt.gca()
ax.set_aspect(1)

# plotte die Zufallspunkte
plt.scatter(*points_array, c=color_array, s=0.1)

plt.xlabel("x")
plt.ylabel("y")

plt.show()

7.6 Übungsaufgabe: Experimentieren mit der MC-Simulation des Wertes von $\pi$¶

Nehmen Sie nun die oben definierte Funktion für die MC-Simulation des Wertes von $\pi$ zur Hand und verändern Sie die Parameter für Anzahl der Runs und Punkte. Können Sie zeigen, dass der numerische Fehler des Means of Sample-Means wie eins durch die Wurzel aus dem Produkt dieser beiden Anzahlen skaliert?

In [13]:

# initialisiere Liste für Ergebnisse für Sigma
sigma_list = []

# definiere Liste für verschiedene Werte für N
n_list = [10, 100, 1000, 10000, 100000, 10000000, 100000000]

# loop über diese Werte von N
for an_n in n_list:

    # rufe die Simulation auf, mit entsprechendem Wert für N
    # die Anzahl der Samples lassen wir gleich
    _, _, ssm_ratios = simulate_value_of_pi(n_samples = 20, n_points = an_n)
    
    # hänge Wert von sigma an die Sammelliste an
    sigma_list.append(ssm_ratios)
    
# gib die Liste aus
print(sigma_list)

100%|██████████| 20/20 [00:00<00:00, 35910.14it/s]
100%|██████████| 20/20 [00:00<00:00, 24485.14it/s]
100%|██████████| 20/20 [00:00<00:00, 12885.73it/s]
100%|██████████| 20/20 [00:00<00:00, 5320.70it/s]
100%|██████████| 20/20 [00:00<00:00, 586.82it/s]
100%|██████████| 20/20 [00:03<00:00,  5.17it/s]
100%|██████████| 20/20 [01:13<00:00,  3.69s/it]

[0.5200000000000001, 0.17385051049680592, 0.050237834348228025, 0.02031333552127766, 0.006852599798616635, 0.0004790655136826607, 0.00014928203326588165]

In [14]:

# stelle das wieder grafisch dar und vergleiche es
# mit einem Plot von 1/sqrt(N)
fig = plt.figure()

# plotte die Liste der Sigmas
plt.plot(n_list, sigma_list, label=("Data"))
plt.plot(n_list, 1/np.sqrt(n_list), label=r"$1/\sqrt{N}$")

# Achsenbeschriftungen
plt.xlabel("N")
plt.ylabel(r"$\sigma$")

# Verwende logarithmische Skalen auf beiden Achsen
# dadurch ist ein Verhalten wie 1/sqrt(N) eine gerade Linie
plt.xscale("log")
plt.yscale("log")

# zeige Legende
plt.legend()

plt.show()

Andreas Krassnigg: Physics, AI and Data Science

AI expert and lecturer at the University of Graz

Monte-Carlo-Methoden – Simulation und Integration