- Startseite
- Allgemeine Informationen zur Lehrveranstaltung
- Einfaches Python Setup und Wichtige Informationen
- 0. Python Einführung und Checkup
- 1. Einführung und einfache Algorithmen
- 2. Differenzieren und Integrieren
- 3. Vektoren, Matrizen und Vektorisierung in Python
- 4. Datenanalyse bzw. Datenauswertung
- 5. Grundlagen der Optimierung und Gradient Descent
- 6. Stochastische Optimierung und Genetische Algorithmen
- 7. Monte-Carlo-Methoden – Simulation und Integration
- 8. Monte-Carlo-Methoden, Teil 2 – Monte-Carlo-Integration, Teil 2 und Random Walk
- 9. Unsupervised Machine Learning: Clustering von Daten
- 10. Supervised Machine Learning: Grundlagen
- 11. Einführung in künstliche neuronale Netzwerke
Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.
5. Grundlagen der Optimierung und Gradient Descent¶
Optimierung begegnet uns nahezu überall in modernen Problemen und interessanten Fragestellungen. Wir werden uns in diesem Notebook mit den Grundlagen der Optimierung befassen und dann auch noch einen konkreten Optimierungs-Algorithmus kennen lernen: Gradient Descent.
5.1 Was ist Optimierung¶
Bei einem Optimierungsproblem geht es grundsätzlich darum, eine bestimmte Größe oder Funktion von Input-Variablen entweder zu maximieren oder zu minimieren. Diese Größe heißt je nach Kontext z.B. “Zielfunktion”, “Kostenfunktion”, “Fitnessfunktion”, etc. Gemeint ist damit aber einfach immer jene Funktion, die optimiert werden soll.
Grundsätzlich kann es bei Optimierungsproblemen verschiedene Einschränkungen geben:
- Die erlaubten Wertebereiche der Input-Variablen können eingeschränkt sein
- Die Wertebereiche der Zielfunktion können eingeschränkt sein
- Die Werte der Input-Variablen können durch eine sogenannte Nebenbedingung zusammenhängen
- Der “Anspruch” der Optimierung kann eingeschränkt sein auf entweder lokale oder globale Optima, die man finden möchte.
Sehen wir uns gleich ein einfaches Beispiel an, dass zwei dieser Einschränkungen aufweist:
Finde jene beiden verschiedenen Zahlen aus der Menge der natürlichen Zahlen bis 10, die folgendes leisten:
- Die Summe der beiden Zahlen muss 10 ergeben
- Das Produkt der beiden Zahlen soll maximal sein
Die eine Einschränkung ist die Nebenbedingung der fixen Summe, die andere Einschränkung ist, dass wir es mit natürlichen Zahlen zu tun haben, also einer diskreten (bzw. letztlich auch endlichen) Menge von möglichen Input-Werten.
Um dieses Problem zu lösen müssten wir eigentlich gar nicht programmieren, sondern nur nachdenken. Aber ich werde trotzdem das Notebook nutzen, um das Beispiel zu illustrieren.
%matplotlib inline
# zunächst die Imports für diese Einheit
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sympy as sp
# gib alle natürlichen Zahlen von 1 bis 10 aus
number_array = np.arange(1,11,1)
print("Kanidaten:", number_array)
# leere Liste, wo alle Paare hineinsollen, die die Bedingungen erfüllen
pair_list = []
# nun gehen wir alle Kombinationen durch
for number_1 in number_array:
for number_2 in number_array:
# überprüfe die Summenvoraussetzung und die Ungleichheit
if (number_1 + number_2 == 10) and (number_1 != number_2):
# das ist interessant, gib die Zahlen und das Produkt aus
print(number_1, "mal", number_2, "ist", number_1 * number_2)
# hänge diese Outputs auch an die Liste an
pair_list.append([number_1, number_2, number_1 * number_2])
# verwandle die Liste in ein Array
pair_array = np.array(pair_list)
# zum Schluss, finde das Maximum in der Liste
optimal_position = np.argmax(pair_array[:, -1])
optimal_solution = pair_array[optimal_position]
print("Die optimale Lösung:", optimal_solution)
Kanidaten: [ 1 2 3 4 5 6 7 8 9 10] 1 mal 9 ist 9 2 mal 8 ist 16 3 mal 7 ist 21 4 mal 6 ist 24 6 mal 4 ist 24 7 mal 3 ist 21 8 mal 2 ist 16 9 mal 1 ist 9 Die optimale Lösung: [ 4 6 24]
5.2 Varianten der Optimierung¶
Hier haben wir also gesehen, wie man, mehr oder weniger mit der Hand und eine nach der anderen, alle Möglichkeiten durchspielt und am Schluss nachsieht, welche Möglichkeit optimal ist. So eine herangehensweise nennt man oft “brute-force” approach, denn mehr als Rechengewalt haben wir nicht verwendet. Insbesondere haben wir folgendes nicht getan:
- Eine Formel verwendet, um die Lösung direkt zu bestimmen
- Einen iterativen Algorithmus verwendet, der von einem Startwert aus Schritt für Schritt immer bessere Lösungsvorschläge liefert
- Die Werte der Input-Variablen eingeschränkt, als wir sie in die Loops geschickt haben
- Aus möglichen Input-Werten per Zufallsprinzip gesampelt, um Rechenzeit zu sparen, aber gleichzeitig trotzdem einen repräsentativen Teil aller Möglichkeiten abzubilden
Diese Dinge sind natürlich grundsätzlich gute Möglichkeiten, um ein Optimierungsproblem zu vereinfachen. Machmal sind sie allerdings sogar unerlässlich, um überhaupt Fortschritte erzielen zu können. Nehmen wir dazu nocheinmal das obige Beispiel zur Hand und stellen wir uns vor, aus 10 würde eine viel größere Zahl.
Aus unserer Zeit-Komplexitäts-Analyse wissen wir noch, dass ein Programm mit zwei Loops bis $N$ zunächst einmal wie $N^2$ skalieren wird. Hier kommt dann noch etwas dazu, nämlich die Suche nach dem Maximum in der entstandenen Liste. Uns geht es hier allerdings nicht so sehr um diese Details, sondern zunächst einmal darum, dass wir (auch von den Primzahlen damals) schon wissen, dass man hier im Prinzip ganz ordentlich einsparen kann, wenn man z.B. die Loops gut einschränken kann.
Wenn wir hier z.B. den inneren Loop nur bis zu 1 unter der aktuellen Zahl im äußeren Loop laufen lassen, dann können wir sogar die Hälfte der if-Abfrage weglassen (nämlich ob die beiden Zahlen gleich sind). Somit ändern wir den Code etwas ab zu:
# wo liegt die Grenze?
n = 1000
number_array = np.arange(1, n+1, 1)
# print("Kanidaten:", number_array)
# leere Liste, wo alle Paare hineinsollen, die die Bedingungen erfüllen
pair_list = []
# nun gehen wir nur mehr die Hälfte aller Kombinationen durch
for number_1 in number_array:
# der Zweite Loop wird jetzt früher abgebrochen
for number_2 in number_array[:number_1-1]:
# überprüfe die Summenvoraussetzung
if (number_1 + number_2 == n):
# das ist interessant, gib die Zahlen und das Produkt aus
# print(number_1, "mal", number_2, "ist", number_1 * number_2)
# hänge diese Outputs auch an die Liste an
pair_list.append([number_1, number_2, number_1 * number_2])
# verwandle die Liste in ein Array
pair_array = np.array(pair_list)
# zum Schluss, finde das Maximum in der Liste
optimal_position = np.argmax(pair_array[:, -1])
optimal_solution = pair_array[optimal_position]
print("Die optimale Lösung:", optimal_solution)
Die optimale Lösung: [ 501 499 249999]
5.3 Optimierung mit kontinuierlichen Variablen¶
Unsere ersten Optimierungserfahrungen in diesem Notebook haben wir also mit diskreten Variablen gemacht. Oft werden Sie allerdings mit kontinuierlichen Variablen (z.B. Koordinaten) zu tun haben. Daher wenden wir uns nun dieser Situation zu und befassen uns gleich auch noch mit einem konkreten iterativen Lösungsalgorithmus dafür.
Zunächst sehen wir uns einmal so ein Problem konkret an einem Beispiel an. Nehmen wir z.B. folgendes:
Gegeben ist die Funktion $f(x, y) = (x – 1)^2 + (y-2)^2 + 1$. Für welche $(x, y)$ ist $f$ minimal?
Dazu noch ein paar Anmerkungen:
- Üblicherweise kann man für Optimierungsprobleme mit kontinuierlichen Variablen die Wertebereiche der Input-Variablen einfach als $\mathbb{R}$ annehmen (oder $\mathbb{R}$, eingeschränkt auf ein Intervall).
- Man muss aufpassen, dass man zwischen lokalen und globalen Optima unterscheidet. Ein lokales Minimum kann man z.B. mit Methoden aus der Differenzialrechung finden. Das muss jedoch nicht unbedingt auch das globale Minimum sein.
- Insbesondere bei der Einschränkung der Input-Werte auf Intervalle muss man von vornherein wissen, ob man (ggf. eher) nach globalen oder lokalen Optima sucht.
In unserem Beispiel suchen wir nach beidem gleichzeitig, denn die beiden sind identisch. Das können wir allerdings nur sagen, weil wir wissen, wie die Funktion in etwa aussieht. Hier ist sie z.B. einmal geplottet:
# definiere f
def our_function(x, y):
# Beachte: Die Argumente können hier Arrays sein
return (x-1)**2 + (y-2)**2 + 1
# definiere x-Werte
x_vals = np.linspace(-1, 3, 50)
# definiere y-Werte
y_vals = np.linspace(0, 4, 50)
# erzeuge x-y-Grid für 3D Plots
X, Y = np.meshgrid(x_vals, y_vals)
Z = our_function(X, Y)
# neue Grafik
fig = plt.figure()
# 3D Achsen erzeugen
ax = fig.add_subplot(1,1,1, projection='3d')
# erzeuge 3D-Oberflächenplot
ax.plot_surface(X, Y, Z, cmap="magma")
plt.show()
So sieht also die Funktion aus. Es gibt auch noch andere Arten, so etwas zu plotten, z.B. diese:
# neue Grafik
fig = plt.figure(figsize=(10, 5))
# 3D Achsen 1 erzeugen
ax1 = fig.add_subplot(1,2,1, projection='3d')
# erzeuge 3D-Oberflächenplot
ax1.scatter(X, Y, Z, s=0.1)
# 2D Achsen 2 erzeugen
ax2 = fig.add_subplot(1,2,2)
# erzeuge 2D-Contourplot
ax2.contour(X, Y, Z, 50, cmap='magma')
plt.show()
Wie kann man nun von so einer Funktion das Minimum finden? Beim Kapitel über Vektoren und Matrizen hatten wir schon einmal so etwas ähnliches, nämlich über die lineare Regression (Zur besseren Erklärung: Dort war die Zielfunktion die Summe aller quadrierten Abstände der Beschreibung von den Datenpunkten).
Wir haben damals die exakte Lösungsformel für den Least-Squares-Fit aufgeschrieben und auch umgesetzt. Das ginge konkret auch bei dieser Form der Funktion (weil sie auch quadratisch ist), aber das geht nicht immer. Konkret muss man sogar sagen, dass sehr viele Optimierungsprobleme bisher keine Lösung in dem Sinn haben, dass kein Algorithmus bekannt ist, der das echte Optimum findet.
Nichtsdestotrotz sind viele dieser Probleme zumindest näherungsweise lösbar, und das ist meist gut genug. Wir werden uns daher hier einem Algorithmus zuwenden, der allgemein einsetzbar ist, und der zumindest näherungsweise Lösungen finden kann.
5.4 Gradient Descent¶
Beim Gradient-Descent-Algorithmus geht es darum, bei einer Minimierungsaufgabe dem Gradienten der (Hyper-)Fläche der Zielfunktion im Raum der Variablen Schritt für Schritt so zu folgen, dass man “immer bergab” geht. Stellen Sie sich vor, Sie stehen an einer riesigen Grube (z.B. einem Meteoritenkrater) und wollen an den tiefsten Punkt kommen. Dann könnten Sie folgendes tun:
- Suchen Sie rund um Ihre Position herum jene Stelle, wo es am meisten bergab geht
- Gibt es überhaupt eine Richtung, in der es bergab geht?
- Ja? Machen Sie einen Schritt in diese Richtung
- Nein? Sie haben ein (lokales) Minimum erreicht
Mathematisch ausgedrückt macht man bei dieser Vorgehensweise folgendes:
- Wählen Sie einen Startpunkt $(x_0, y_0)$
- Wählen Sie eine Schrittweite $a$
- Berechnen Sie dort den Gradienten $\nabla f(x, y)|_{(x=x_0, y=y_0)}$
- Berechnen Sie den nächsten Punkt, einen Schritt vom vorigen Punkt entfert, entlang des negativen Gradienten, also $$(x_1, y_1) = (x_0, y_0) – a \nabla f(x, y)|_{(x=x_0, y=y_0)}$$
- Nutzen Sie jetzt $(x_1, y_1)$ als neuen Startpunkt für den nächsten Schritt und wiederholen Sie das, bis die Abbruchbedingung erfüllt ist
- Abbruchbedingung: Eine vorgegebene maximale Anzahl von Schritten oder irgendwann ist $||(x_n, y_n)-(x_{n-1}, y_{n-1})||<\varepsilon$ für eine vorgegebene Genauigkeit $\varepsilon$.
Wir wollen nun diesen Algorithmus für unser obiges konkretes Beispiel durchgehen.
# definiere zwei Variablen x und y über SymPy
x, y = sp.symbols('x, y')
# definiere die Funktion f
f = (x-1)**2 + (y-2)**2 + 1
# Startwert
x0 = np.array([0.5, 1.])
# übergebe an wachsendes Array für den Pfad
xy = np.array([x0])
# Schrittweite
a = 0.1
# Loop über Schritte (wir lassen hier den Genauigkeitscheck einfach mal weg)
for ind in range(100):
# hole den letzten Punkt aus der Punkteliste (Pfad)
present_point = xy[-1]
# schreibe den momentanen Punkt heraus
print(present_point)
# berechne den Gradienten and dieser Stelle
gradi = np.array([sp.diff(f, x).subs(x, present_point[0]).subs(y, present_point[1]),
sp.diff(f, y).subs(x, present_point[0]).subs(y, present_point[1])])
# mache einen Gradient-Descent Schritt, also ziehe den Gradienten mal Schrittweite
# vom derzeitigen Punkt ab
# hänge dann das Resultat an das xy-Array an
xy = np.append(xy, np.reshape(present_point - a * gradi, (1, 2)), axis=0)
[0.5 1. ] [0.600000000000000 1.20000000000000] [0.680000000000000 1.36000000000000] [0.744000000000000 1.48800000000000] [0.795200000000000 1.59040000000000] [0.836160000000000 1.67232000000000] [0.868928000000000 1.73785600000000] [0.895142400000000 1.79028480000000] [0.916113920000000 1.83222784000000] [0.932891136000000 1.86578227200000] [0.946312908800000 1.89262581760000] [0.957050327040000 1.91410065408000] [0.965640261632000 1.93128052326400] [0.972512209305600 1.94502441861120] [0.978009767444480 1.95601953488896] [0.982407813955584 1.96481562791117] [0.985926251164467 1.97185250232893] [0.988741000931574 1.97748200186315] [0.990992800745259 1.98198560149052] [0.992794240596207 1.98558848119241] [0.994235392476966 1.98847078495393] [0.995388313981573 1.99077662796315] [0.996310651185258 1.99262130237052] [0.997048520948207 1.99409704189641] [0.997638816758565 1.99527763351713] [0.998111053406852 1.99622210681370] [0.998488842725482 1.99697768545096] [0.998791074180385 1.99758214836077] [0.999032859344308 1.99806571868862] [0.999226287475447 1.99845257495089] [0.999381029980357 1.99876205996071] [0.999504823984286 1.99900964796857] [0.999603859187429 1.99920771837486] [0.999683087349943 1.99936617469989] [0.999746469879954 1.99949293975991] [0.999797175903963 1.99959435180793] [0.999837740723171 1.99967548144634] [0.999870192578537 1.99974038515707] [0.999896154062829 1.99979230812566] [0.999916923250263 1.99983384650053] [0.999933538600211 1.99986707720042] [0.999946830880169 1.99989366176034] [0.999957464704135 1.99991492940827] [0.999965971763308 1.99993194352662] [0.999972777410646 1.99994555482129] [0.999978221928517 1.99995644385703] [0.999982577542814 1.99996515508563] [0.999986062034251 1.99997212406850] [0.999988849627401 1.99997769925480] [0.999991079701921 1.99998215940384] [0.999992863761537 1.99998572752307] [0.999994291009229 1.99998858201846] [0.999995432807383 1.99999086561477] [0.999996346245907 1.99999269249181] [0.999997076996725 1.99999415399345] [0.999997661597380 1.99999532319476] [0.999998129277904 1.99999625855581] [0.999998503422323 1.99999700684465] [0.999998802737859 1.99999760547572] [0.999999042190287 1.99999808438057] [0.999999233752230 1.99999846750446] [0.999999387001784 1.99999877400357] [0.999999509601427 1.99999901920285] [0.999999607681141 1.99999921536228] [0.999999686144913 1.99999937228983] [0.999999748915931 1.99999949783186] [0.999999799132745 1.99999959826549] [0.999999839306196 1.99999967861239] [0.999999871444957 1.99999974288991] [0.999999897155965 1.99999979431193] [0.999999917724772 1.99999983544954] [0.999999934179818 1.99999986835964] [0.999999947343854 1.99999989468771] [0.999999957875083 1.99999991575017] [0.999999966300067 1.99999993260013] [0.999999973040053 1.99999994608011] [0.999999978432043 1.99999995686409] [0.999999982745634 1.99999996549127] [0.999999986196507 1.99999997239301] [0.999999988957206 1.99999997791441] [0.999999991165765 1.99999998233153] [0.999999992932612 1.99999998586522] [0.999999994346089 1.99999998869218] [0.999999995476872 1.99999999095374] [0.999999996381497 1.99999999276299] [0.999999997105198 1.99999999421040] [0.999999997684158 1.99999999536832] [0.999999998147327 1.99999999629465] [0.999999998517861 1.99999999703572] [0.999999998814289 1.99999999762858] [0.999999999051431 1.99999999810286] [0.999999999241145 1.99999999848229] [0.999999999392916 1.99999999878583] [0.999999999514333 1.99999999902867] [0.999999999611466 1.99999999922293] [0.999999999689173 1.99999999937835] [0.999999999751338 1.99999999950268] [0.999999999801071 1.99999999960214] [0.999999999840857 1.99999999968171] [0.999999999872685 1.99999999974537]
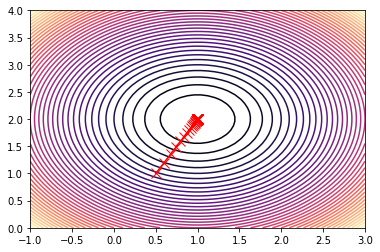
# sehen wir uns das an
fig = plt.figure()
# 2D Achsen 2 erzeugen
ax = fig.add_subplot(1,1,1)
# erzeuge 3D-Oberflächenplot
ax.contour(X, Y, Z, 50, cmap='magma')
# erzeuge x und y Werte aus dem Pfad
x_vals, y_vals = np.transpose(xy)
# Plotte zusätzlich den Pfad
ax.plot(x_vals, y_vals, "rx-", markersize=10)
# Plot anzeigen
plt.show()
5.5 Übungsaufgabe: Spielen Sie mit dem Gradient-Descent-Algorithmus und dem Plot¶
Kopieren Sie nun einfach die relevanten Code-Schnipsel von oben und probieren Sie folgende Dinge aus:
- Nehmen Sie eine andere Funktion $f(x, y)$ und probieren Sie aus, was passiert
- Passen Sie auch die Wertebereiche für $x$ und $y$ entsprechend an, sodass Sie im Plot sehen, wo der Algorithmus hinläuft
- Experimentieren Sie auch mit der Schrittgröße:
- Was passiert, wenn $a$ zu klein gewählt wird?
- Was passiert, wenn $a$ zu groß gewählt wird?
- Finden Sie eine Funktion $f$, für die dieser Algorithmus nicht konvergiert?
# definiere eine andere Funktion g
g = sp.sin((x-1)**2 + (y-2)**2)**2
# Startwert
x0 = np.array([0.5, 0.7])
# übergebe an wachsendes Array für den Pfad
xy = np.array([x0])
# Schrittweite
a = 0.05
# Loop über Schritte (wir lassen hier den Genauigkeitscheck einfach mal weg)
for ind in range(20):
# hole den letzten Punkt aus der Punkteliste (Pfad)
present_point = xy[-1]
# schreibe den momentanen Punkt heraus
print(present_point)
# berechne den Gradienten and dieser Stelle
gradi = np.array([sp.diff(g, x).subs(x, present_point[0]).subs(y, present_point[1]),
sp.diff(g, y).subs(x, present_point[0]).subs(y, present_point[1])])
# mache einen Gradient-Descent Schritt, also ziehe den Gradienten mal Schrittweite
# vom derzeitigen Punkt ab
# hänge dann das Resultat an das xy-Array an
xy = np.append(xy, np.reshape(present_point - a * gradi, (1, 2)), axis=0)
[0.5 0.7] [0.466344453382822 0.612495578795337] [0.415245169591515 0.479637440937938] [0.366802144251622 0.353685575054217] [0.362967067753874 0.343714376160073] [0.363922628571257 0.346198834285268] [0.363675839385038 0.345557182401098] [0.363739067151797 0.345721574594672] [0.363722833570249 0.345679367282647] [0.363726999246876 0.345690198041878] [0.363725930149461 0.345687418388598] [0.363726204517477 0.345688131745440] [0.363726134104344 0.345687948671293] [0.363726152174955 0.345687995654882] [0.363726147537365 0.345687983597150] [0.363726148727543 0.345687986691611] [0.363726148422099 0.345687985897458] [0.363726148500487 0.345687986101267] [0.363726148480370 0.345687986048962] [0.363726148485533 0.345687986062385]
# passe Plotbereiche an
# definiere x-Werte
x_vals = np.linspace(0, 2, 250)
# definiere y-Werte
y_vals = np.linspace(0, 3, 250)
# erzeuge x-y-Grid für 3D Plots
X, Y = np.meshgrid(x_vals, y_vals)
# erzeuge Funktion für numerische Auswertung automatisch
# sodass sie für den Plot übereinstimmt
g_num = sp.lambdify([x, y], g)
# erzeuge Z-Werte über die lambdifizierte Funktion g
Z = g_num(X, Y)
# sehen wir uns auch das an
fig = plt.figure()
# 2D Achsen 2 erzeugen
ax = fig.add_subplot(1,1,1)
# erzeuge 3D-Oberflächenplot
ax.contour(X, Y, Z, 50, cmap='magma')
# erzeuge x und y Werte aus dem Pfad
x_vals, y_vals = np.transpose(xy)
# Plotte zusätzlich den Pfad
ax.plot(x_vals, y_vals, "rx-", markersize=10)
# Plot anzeigen
plt.show()