Die Jupyter-Notebooks zur Lehrveranstaltung finden Sie im zugehörigen GitHub-Repository.

Einführung und einfache Algorithmen

1 Einführung und einfache Algorithmen¶

Algorithmen sind etwas, das wir ständig verwenden. Ob im täglichen Leben oder in speziellen Situationen wie z.B. beim Lösen konkreter Probleme.

Simple Beispiele für Algorithmen sind

Wie man zwei Zahlen miteinander multipliziert
Wie man eine Tasse Tee trinkt
wie Sie sich in unserem Online-Raum (BigBlueButton in Moodle) einfinden
Wie Sie Ihr Studium beenden können/werden

Was alle Algorithmen gemeinsam haben, sind folgende Eigenschaften:

Eine konkrete Abfolge von endlich vielen Schritten
Eine Definition über mehr oder weniger formale Beschreibung, z.B. Pseudocode oder Flowcharts
Eigenschaften, die beim Einteilen in Kategorien helfen
Z.B. einen bestimmten Grad an Komplexität

Im Folgenden werden wir uns ein paar sehr einfache Beispiele ansehen (und gleichzeitig noch ein bisschen Python wiederholen). Sie sollen dabei ein Gefühl dafür bekommen, was mit dem Begriff “Algorithmus” gemeint ist und wie er mit einem Computerprogramm zusammenhängt.

1.1 Einfaches Beispiel: Addieren aller natürlichen Zahlen bis zu einer bestimmten Zahl N¶

Zum Addieren aller natürlichen Zahlen bis zu einer bestimmten Zahl N kann man eine vorberechnete Formel verwenden. Das ist zwar auch ein Algorithmus (multipliziere N mit ihrem Nachfolger N+1 und dividiere durch 2), wir wollen das hier allerdings nicht tun. Wir werden stattdessen einen iterativen Algorithmus verwenden, den wir zuerst mit einer FOR und dann nocheinmal, aber mit einer WHILE Schleife, umsetzen werden.

In [1]:

# Addiere alle natürlichen Zahlen bis zu N

# Importiere die Package NumPy
import numpy as np

# setze die Zahl fest, bis zu der summiert werden soll
N = 10

# initialisiere den Wert der Summe
thesum_1 = 0

# starte for-Loop von 1 bis N. Achtung: In Python endet eine range 
# bereits bei der Zahl vor dem zweiten Argument. Daher müssen wir N+1 schreiben
for summand in np.arange(1, N+1, 1):
    
    # Ausgabe zur Illustration
    print("Addiere ", summand)
    
    # Addiere den aktuellen Summanden
    thesum_1 += summand   # das ist kurz-Schreibweise für thesum_1 = thesum_1 + summand 
    

# Ausgabe des Resultats mit Loop 1
print("Resultat mit for-Loop: ", thesum_1, "\n")


# Initialisiere den Wert der zweiten Summe
thesum_2 = 0

# Setze Summand auf den Anfangswert
summand = 1

# Starte den while-Loop
while summand <= 10:
    
    # Ausgabe zur Illustration
    print("Addiere ", summand)
    
    # Addiere den aktuellen Summanden
    thesum_2 += summand
    
    # Erhöhe den Wert des Summanden um 1
    summand += 1
    

# Ausgabe des Resultats mit Loop 2
print("Resultat mit while-Loop: ", thesum_2, "\n")

    

Addiere  1
Addiere  2
Addiere  3
Addiere  4
Addiere  5
Addiere  6
Addiere  7
Addiere  8
Addiere  9
Addiere  10
Resultat mit for-Loop:  55 

Addiere  1
Addiere  2
Addiere  3
Addiere  4
Addiere  5
Addiere  6
Addiere  7
Addiere  8
Addiere  9
Addiere  10
Resultat mit while-Loop:  55

Schreiben wir das nun nochmals als Algorithmus auf, und zwar anhand der Variante für den FOR-Loop:

Ziel: Finden der Summe aller natürlichen Zahlen bis zu einer bestimmten Zahl N

Input: Diejenige Zahl N, bis zu der man die natürlichen Zahlen aufaddieren möchte

Output: Die Summe aller natürlichen Zahlen bis N

Implementierung: Iterativ

Variablen und Startwerte: Summe = 0, Summand = 1

Iterationsvorschrift: Nimm den nächsten Wert von Summand und addiere diesen zu Summe

Abbruchbedingung: Der Wert von Summand erreicht N

Resultat: Der Output ist der Wert von Summe nach Eintreten der Abbruchbedingung

Das erscheint vielleicht etwas übertrieben, aber im Wesentlichen ist diese Beschreibung nötig, um zu wissen, was man bzw. der Algorithmus tun soll.

Diese Notwendigkeit wird vor allem dann deutlich, wenn man versucht, selbst ein Computerprogramm zu schreiben, das die entsprechende Aufgabe erledigen soll. Im Prinzip musste ich diese Dinge bereits wissen oder mir denken, damit ich das obige Programm schreiben konnte.

Wenn es Ihnen also einmal schwer fällt, ein Python- (oder sonstiges Computer-)Programm für einen bestimmten Zweck zu schreiben, dann machen Sie sich bewusst, was den gerade angegebenen Schritten bzw. der Information für Ihr konkretes Problem entspricht.

1.2 Einfaches Beispiel: Berechnen der ersten N Primzahlen ¶

Dieses Problem war bereits am Ende von Einheit 0 unser Thema. Hier wollen wir es nochmal aufrollen, inklusive einer etwas genaueren Beschreibung als Algorithmus. Außerdem wollen wir uns anhand dieses Beispiels bereits einen Aspekt ansehen, der für computergestützte Algorithmen wichtig sein kann: Die Optimierung des Algorithmus.

Wir werden daher zunächst eine Version beschreiben und ausprobieren, welche die Aufgabe löst, aber nicht unbedingt optimiert ist. Danach werden wir uns ansehen, was man tun kann, um den Algorithmus und damit auch die entprechende Problemlösung besser und schneller zu machen.

Die Aufgabenstellung lautet: Berechne die ersten 1000 Primzahlen (allgemein: berechne die ersten N Primzahlen).

Dazu muss man der Reihe nach alle natürlichen Zahlen untersuchen und feststellen, ob sie durch eine kleinere Zahl außer 1 teilbar sind.

Um dies zu berechnen, werden wir zwei Loops brauchen:

Einen WHILE-Loop, mit dem wir eine natürliche Zahl nach der anderen untersuchen
Einen FOR-Loop, mit dem wir für jede natürliche Zahl alle kleineren Zahlen als mögliche Teiler testen

Zahlen, die keine Teiler haben, kommen in die Primzahl-Liste. Hier ist also die direkte, einfache Version dieses Programms:

In [2]:

%%time    
# lasse einen Timer mitlaufen, umd einen Vergleichswert zu haben

# außerdem importieren wir noch eine time-Package, für die spätere Nutzung
import time

# definiere diese Ausführung als Funktion, um sie später besser nutzen zu können
def get_primes(upto_n):
    
    # speichere die Beginnzeit für später
    start_time = time.time()

    # erstelle eine leere Liste, in die die Primzahlen kommen sollen
    list_of_primes = []

    # definiere den ersten Kandidaten (wir fangen bei 2 an)
    candidate = 2

    # starte den while-Loop. Er läuft, bis die Länge der Primzahlliste N erreicht hat
    while len(list_of_primes) < upto_n:

        # setze den Status als Primzahl vorerst auf True. 
        # Wenn wir einen Teiler finden, setzen wir ihn auf False
        is_prime = True

        # starte den for-Loop. Er läuft von 2 bis zum momentanen Kandidaten minus 1
        # denn eine Primzahl ist nur durch 1 und sich selbst teilbar
        for a_number in range(2, candidate, 1):

            # check, ob der momentane Kandidat durch die Versuchszahl teilbar ist
            if (candidate % a_number == 0):
                
                # ja, ist teilbar, setze den Status auf False
                is_prime = False

        # wenn alle Zahlen kleiner der Kandidatenzahl durchprobiert sind, checken wir den Status
        if is_prime:
            
            # ja, ist noch auf True. Hänge den Kandidaten an die Primzahlliste an
            list_of_primes.append(candidate)

        # gehe zur nächsten natürlichen Zahl weiter
        candidate += 1 
    
    # Bestimme die Zeit, zu der die Berechnung zu Ende war
    end_time = time.time()
    
    # Berechne die Dauer der Primzahl-Berechnung
    run_time = end_time - start_time

    # Zurückgeben der Liste
    return list_of_primes, run_time


# Rufe die Funktion auf
result_list, the_time = get_primes(1000)

# gib die Liste aus
print(result_list)

# und checke die Länge der Liste
print("Anzahl der Primzahlen in dieser Liste: ", len(result_list))

# gib auch die Runtime aus
print("Runtime der Funktion: ", the_time)

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057, 4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139, 4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231, 4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297, 4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409, 4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493, 4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583, 4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657, 4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751, 4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831, 4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937, 4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003, 5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087, 5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179, 5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279, 5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387, 5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443, 5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521, 5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639, 5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693, 5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791, 5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857, 5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939, 5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053, 6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133, 6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221, 6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301, 6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367, 6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473, 6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571, 6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673, 6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761, 6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833, 6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917, 6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997, 7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103, 7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207, 7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297, 7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411, 7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499, 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829, 7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919]
Anzahl der Primzahlen in dieser Liste:  1000
Runtime der Funktion:  1.716271162033081
CPU times: user 1.71 s, sys: 6.19 ms, total: 1.71 s
Wall time: 1.72 s

Nach dieser ersten Variante, die zwar den Zweck erfüllt, aber verbesserungsfähig ist, kommen wir nun zu ein paar Schritten der Optimierung.

Die Grundidee dabei ist, anstatt aller Zahlen, die kleiner als der momentane Primzahlkandidat n sind, als mögliche Teiler anzusehen, eine Liste mit Primzahlen nach und nach zu erstellen, und diese auch für die Berechnung weiterer Primzahlen zu benutzen. Dabei kann man folgende Punkte beachten und verwenden:

Alle Primzahlen bis auf die erste, 2, sind ungerade.
Als mögliche Teiler weiterer Primzahlkandidaten muss man nur bisherige Primzahlen in Betracht ziehen, denn wenn ein Kandidat durch eine kleinere Zahl teilbar ist, dann ist er auch durch alle Primfaktoren jener kleineren Zahl teilbar, und diese Faktoren kommen beim Check vorher dran.
Für einen bestimmten Kandidaten n braucht man nur mögliche Teiler bis zur Quadradwurzel aus n zu testen, denn es kann keinen größeren Teiler geben, ohne dass es auch einen kleineren Teiler gibt, den man dann bereits gefunden haben müsste.

In [3]:

%%time
# lasse einen Timer mitlaufen, umd einen Vergleichswert zu haben

# definiere diese Ausführung als Funktion, um sie später besser nutzen zu können
def get_primes_faster(upto_n):

    # speichere die Beginnzeit für später
    start_time = time.time()

    # starte mit der bereits mit 2 vorbefüllten Liste
    list_of_primes = [2]

    # definiere die Länge der Liste als Variable
    total_number = len(list_of_primes)

    # setze den ersten Kandidaten auf 3
    candidate = 3

    # starte den while-Loop bis N
    while total_number < upto_n:

        # setze den Prime-Status auf True
        is_prime = True

        # starte den for-Loop, diesmal nur über die bisher gefundenen Primzahlen als mögliche Teiler
        for a_prime in list_of_primes:

            # check, ob wir schon bei der Quadradwurzel aus der Kandidatenzahl angelangt sind
            if a_prime > np.sqrt(candidate):

                # wenn ja, brich den for-Loop ab
                break

            # check der Teilbarkeit durch den Test-Primzahl-Teiler
            if (candidate % a_prime == 0):

                # ja, ist teilbar, setze den Status auf False
                is_prime = False

                # und brich den for-Loop ab
                break

        # checke den Status
        if is_prime:

            # ist eine Primzahl, wird an die Liste angehängt
            list_of_primes.append(candidate)

        # erzeuge die neue Länge der Primzahlliste
        total_number = len(list_of_primes) 

        # erhöhe die Kandidaten-Zahl um 2 (nur ungerade Zahlen werden als Kandidaten zugelassen)
        candidate += 2

    # bestimme die End-Zeit der Berechnung
    end_time = time.time()
    
    # Berechne die Dauer
    run_time = end_time - start_time

    # Zurückgeben der Liste
    return list_of_primes, run_time


# Rufe die Funktion auf
result_list, the_time = get_primes_faster(1000)

# gib die Liste aus
print(result_list)

# und checke die Länge der Liste
print("Anzahl der Primzahlen in dieser Liste: ", len(result_list))     

# gib auch die Runtime aus
print("Runtime der Funktion: ", the_time)

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057, 4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139, 4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231, 4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297, 4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409, 4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493, 4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583, 4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657, 4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751, 4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831, 4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937, 4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003, 5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087, 5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179, 5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279, 5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387, 5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443, 5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521, 5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639, 5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693, 5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791, 5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857, 5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939, 5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053, 6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133, 6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221, 6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301, 6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367, 6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473, 6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571, 6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673, 6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761, 6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833, 6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917, 6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997, 7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103, 7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207, 7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297, 7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411, 7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499, 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829, 7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919]
Anzahl der Primzahlen in dieser Liste:  1000
Runtime der Funktion:  0.03052973747253418
CPU times: user 30.6 ms, sys: 476 µs, total: 31.1 ms
Wall time: 30.8 ms

Wie man anhand der Timings sehen kann, ist die zweite Variante wesentlich effizienter.

Der hier verwendete Zugang, eine Art Rapid Prototyping, wird auch in der Praxis oft angewandt. Zunächst schreibt man ein Programm, von dem man einmal eine Antwort bekommt – egal wie langsam – , und danach versucht man, es zu optimieren.

1.3 Zeit-Komplexität¶

Ein Aspekt, der hier interessant ist, bezieht sich auf die Zeit, die ein Algorithmus für die Ausführung seiner Aufgabe braucht. Normalerweise wird das als Funktion der relevanten Input-Variablen betrachtet. In unserem Fall wäre das z.B. für die Primzahlen die gewünschte Anzahl N von Primzahlen.

Der Begriff der Zeit-Komplexität selbst ist recht komplex. Z.B. hängt die Laufzeit eines Programms von der Hardware ab, von der Last, die bereits auf dieser Hardware läuft, von Details der Implementierung, diversen Faktoren in der Programmierung, etc. Wir können und werden das hier daher nicht im Detail diskutieren, sondern werden uns diesem Begriff einfach ganz intuitiv nähern, und zwar auf eine Art und Weise, die von solchen Details weitgehend unabhängig ist.

Um das zu tun, werden wir die beiden Implementierungen von oben vergleichen, und zwar, was ihr Skalierungsverhalten mit N betrifft. Damit ist folgendes gemeint: Wir werden beide Implementierungen für verschiedene N laufen lassen, die gebrauchten Zeiten messen und diese als Funktion von N erst einmal grafisch darstellen.

Beginnen wir mit der einfacheren aber langsameren der beiden Varianten:

In [4]:

%matplotlib inline

# importiere Matplotlib
import matplotlib.pyplot as plt


# Erzeuge eine Liste mit den gewünschten N Werten
# n_list_slower = np.arange(10, 500, 50)

# Eine umfangreichere Möglichkeit:
n_list_slower = np.append(np.arange(10, 100, 10), [200, 300, 500, 1000, 3000])

# Erzeuge leere Liste für die Timings
time_list_slower = []

# Loop über alle N in der Liste
for an_n in n_list_slower:
    
    # Rufe die Funktion auf und erhalte das Ergebnis samt Timing
    result_list, the_time = get_primes(an_n)
    
    # Schreibe das Timing in die Zeiten-Liste dazu
    time_list_slower.append(the_time)
    

# Grafische Darstellung der Ergebnisse
fig = plt.figure()

# plot-Befehl
plt.plot(n_list_slower, time_list_slower, "x-")

# Achsenbeschriftungen und Titel
plt.xlabel("N")
plt.ylabel("Zeit [s]")
plt.title("Skalierungsverhalten für Primzahlenberechnung")

# Skalierungen der Achsen von linear auf logarithmisch setzen
plt.xscale("log")  # auskommentieren, um eine lineare Darstellung in x zu erhalten
plt.yscale("log")  # auskommentieren, um eine lineare Darstellung in y zu erhalten

# Grafik anzeigen
plt.show()

Hier sieht man schon ganz gut, dass sich ein bestimmtes Verhalten abzeichnet. Je nach Skalierung der x- und y-Achse (log oder linear) kann man die Kurve betrachten und sich überlegen, um welche funktionelle Abhängigkeit es sich dabei handeln könnte.

Konkret sieht man bei einer log-log Darstellung (also x-Achse und y-Achse beide mit logarithmischer Skala) ein halbwegs lineares Verhalten. So etwas entspricht einem Polynomialen verhalten. Die größte Potenz im Polynom kann man im Prinzip sogar direkt aus dem Plot über die Steigung der Kurve (bzw. idealerweise der Geraden) bestimmen.

Wir werden uns jetzt der zweiten Implementierung zuwenden, dabei aber gleich auch ein paar solche Möglichkeiten als Vergleichskurven mit in den Plot einbauen.

In [5]:

# Erzeuge eine Liste mit den gewünschten N Werten
n_list = np.arange(10, 5000, 100)
# n_list = np.array([10, 100, 1000, 10000]) # Alternative für direkte Eingabe

# Eine Liste für den Skalierungsvergleich, mit N Sqrt(N)
comp_list = np.sqrt(n_list) * n_list / 1000000

# Eine Liste für den Skalierungsvergleich, mit N**2
comp_list_slow = n_list**2 / 400000

# Eine Liste für den Skalierungsvergleich, mit N**2
#comp_list_slow_1 = np.sqrt(n_list) * n_list / 4000    # Aktivieren, um den Vergleich mit dem anderen Scaling zu sehen

# Erzeuge leere Liste für die Timings
time_list = []

# Loop über alle N in der Liste
for an_n in n_list:
    
    # Rufe die Funktion auf und erhalte das Ergebnis samt Timing
    result_list, the_time = get_primes_faster(an_n)
    
    # Schreibe das Timing in die Zeiten-Liste dazu
    time_list.append(the_time)
    

# Grafische Darstellung der Ergebnisse
fig = plt.figure()

# Daten der schnelleren Variante
plt.plot(n_list, time_list, "g", label="Data")

# Vergleichs-Skalierung
plt.plot(n_list, comp_list, "r", label=r"$\mathcal{O}(N\sqrt{N})$")

# Daten der langsameren Variante
plt.plot(n_list_slower, time_list_slower, "b", label="Slower Data")

# Vergleichs-Skalierung
plt.plot(n_list, comp_list_slow, "r--", label=r"$\mathcal{O}(N^2)$")
# plt.plot(n_list, comp_list_slow_1, "r.", label=r"$\mathcal{O}(N\sqrt{N})$")  # Aktivieren, um den Vergleich mit dem anderen Scaling zu sehen

# Achsenbeschriftung und Titel
plt.xlabel("N")
plt.ylabel("Zeit [s]")
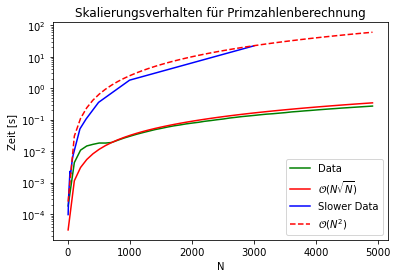
plt.title("Skalierungsverhalten für Primzahlenberechnung")

# Log-Skala für y und Platzierung der Legende
plt.yscale("log")
plt.legend(loc=4)

plt.show()

Was sich hier zeigt, sind folgende Punkte:

Das Verhalten der Berechnung nach den beiden Implementationen des Algorithmus lässt sich gut grafisch darstellen
Mit Vorüberlegungen bezüglich der zu erwartenden Skalierung kann man auch Vergleichskurven plotten
Die erste, langsamere Implementierung beinhaltet zwei Loops, die beide im wesentlichen bis $N$ gehen. Die Berechnung skaliert daher von der Erwartung her wie $N^2$.
Die zweite, effizientere Implementierung beinhaltet einen Loop bis $N$, der andere geht nur bis zur Quadratwurzel aus $N$, woher man sich die veränderte Skalierung überlegen kann.
Wenn man versucht, die Skalierung der zweiten Variante über die Daten der ersten zu legen, hat man Schwierigkeiten, eine gute Übereinstimmung zu erreichen.

Skalierungen, wie wir sie hier gesehen haben, nennt man polynomial, d.h., wie ein Polynom (von grundsätzlich beliebigem Grad) in $N$. Andere Skalierungen bzw. Komplexitätsklassen, die interessant sind, sind z.B.:

$1$ : Das bedeutet konstante Zeit als Funktion von $N$ (z.B. Berechnung von $(-1)^N$)
$N$ : Das bedeutet lineare Abhängigkeit von $N$ (z.B. finden des Maximums eines unsortierten Arrays)
$\log(N)$ : Das bedeutet logarithmische Abhängigkeit von $N$ (z.B. Binäre Suche – finden der Position eines bestimmten Werts in einem sortierten Array)
$2^{poly(N)}$ : Das bedeutet exponentielle Abhängigkeit von $N$ (z.B. brute-force Analyse der Matrix-Ketten-Multiplikation)

Sie sollen sich nicht unbedingt die einzelnen Fälle merken, aber sehr wohl die verschiedenen Kategorien. Beachten Sie, dass ein und dasselbe Problem je nach Lösungsmethode in verschiedene Klassen gehören kann. Sie sollten in erster Linie wissen, dass man beim algorithmischen Lösen von Problemen in zeitliche Limits laufen kann. Das gilt übrigens auch für andere Faktoren wie z.B. Arbeitsspeicher (Platzkomplexität).

1.4 Übungsaufgabe: Implementieren Sie eine einfache Version des Newton-Raphson Verfahrens zum Finden einer Nullstelle einer Funktion¶

Zur Vorbereitung dieser Aufgabe finden Sie im Folgenden die nötigen Details der Netwon-Raphson-Methode.

Die Newton-Raphson-Methode (oder kurz das Newton-Verfahren) basiert darauf, dass man für eine gegebene Funktion eine Nullstelle in der Nähe eines Anfangswertes sucht, indem man am Anfangswert für $x$ die Tangente an die Kurve von $f(x)$ konstruiert und diese mit der $x$-Achse schneidet. Dieser Schnittpunkt wird zum nächsten Näherungswert für die Nullstelle. Dort konstruiert man wieder die Tangente an die Kurve, schneidet diese mit der $x$-Achse, und so weiter. Das macht man so lange, bis sich die Näherungswerte von einem Schritt zum nächsten nicht um mehr unterscheiden als eine vorgegebene Genauigkeit (am besten relativ).

Soweit, so gut. Konkret implementiert man das folgende iterativen Verfahren:

Bestimmen Sie einen Anfangswert $x_0$. Dieser liegt idealerweise bereits in der Nähe der Lösung, die man sucht. Das muss zwar nicht zwingend der Fall sein, es ist aber möglich, dass das Verfahren für bestimmte Bereiche von Anfangswerten nicht konvergiert. Solche Probleme hängen von der untersuchten Funktion ab.
Schreiben Sie die Funktion als $f(x)$ und deren erste Ableitung nach $x$ als $f'(x)$ explizit an. (Sollte das nicht möglich sein, dann kann man auch numerische Berechnungsverfahren für die Ableitungen verwenden.
Implementieren Sie die folgende Iterationsformel: $x_{i+1} = x_i – f(x_i) / f'(x_i)$. (Wenn Sie möchten und Zeit dafür haben, können Sie sich auch davon überzeugen, dass diese Vorschrift tatsächlich die Nullstelle der Tangente von $f(x)$, an der Stelle $x_i$ an $f$ angelegt, liefert.
Definieren Sie einen geeigneten Faktor für eine relative Genauigkeit für das Näherungsergebnis
Implementieren Sie einen Loop, der die Iterationsformel so lange ausführt, bis die gewünschte Genauigkeit erreicht ist.
Begrenzen Sie den Loop zusätzlich mit einer maximalen Anzahl von Schritten, sodass es bei Divergenz des Newton-Verfahrens zu keinen Problemen kommt

Diese Schritte sollten sich relativ direkt in Python implementieren lassen. Als einfaches Beispiel einer Funktion für diese Aufgabe schlage ich Ihnen vor, $f(x) = x^2 – 2$ zu verwenden. Wie Sie sich recht einfach selbst überzeugen können, liegt eine Nullstelle dieser Funktion bei der Quadratwurzel aus $2$. Dieses Ergebnis lässt sich also recht gut überprüfen. Sie können aber natürlich gerne auch andere Funktionen untersuchen und deren Nullstellen finden.

Zusatzaufgabe (optional): Wenn Sie ein erfolgreiches Beispiel durchexerziert haben, können Sie sich auch überlegen, welche Situation eigentlich zur Divergenz des Verfahrens führt. Offensichtlich ist aus der Interationsbedingung, dass man Extremwerte nicht in der Folge der $x_i$ haben darf (denn sonst dividiert man durch $0$). Aber was mit Divergenz hauptsächlich gemeint ist, ist eine Situation, in der die $x_i$ nicht immer näher an die Nullstelle heranrücken, sondern immer weiter weg wandern. Wie kann man so etwas erreichen?

In [6]:

# Beispiellösung:

# Setze Anfangswert für x_0
x0 = 1.

# Setze x_0 auch als vergangenen Wert für die Iteration an
x_prev = x0

# Setze relative Zielgenauigkeit
eps = 1.e-6

# Setze Maximalwert für Iterationen im while-Loop
nmax = 1000

def f(x):
    # definiere Funktion, von der wir Nullstellen finden wollen
    return x**2 - 2.

def fprime(x):
    # definiere Ableitung dieser Funktion
    return 2*x


# Setze Counter zum Verfolgen der Iterationsschritte
icount = 1

# Setze Schrittvergleich auf etwas großes
the_change = 1.

# starte while-Loop
while icount < nmax and the_change > eps:
    
    # Berechne relative Änderung
    the_change = np.abs(f(x_prev)/fprime(x_prev)/x_prev)
    
    # Iterationsvorschrift
    x_next = x_prev - f(x_prev)/fprime(x_prev)
    
    # Ausgabe der Werte für diesen Schritt in der Iteration
    print("Schritt ", icount)
    print("Relative Änderung: ", the_change)
    print("Neuer Näherungswert: ", x_next)
    
    # Übergeben des Neuen Wertes in den nächsten Durchlauf der Schleife
    x_prev = x_next
    
    # Erhöhe den Schritt-Counter
    icount += 1
    
    
# Schluss-Output nach Beendigung des While-Loops
print("Das Ergebnis ist ", x_next)
print("Check: ", np.sqrt(2.))
    

Schritt  1
Relative Änderung:  0.5
Neuer Näherungswert:  1.5
Schritt  2
Relative Änderung:  0.05555555555555555
Neuer Näherungswert:  1.4166666666666667
Schritt  3
Relative Änderung:  0.0017301038062284225
Neuer Näherungswert:  1.4142156862745099
Schritt  4
Relative Änderung:  1.5018217097673717e-06
Neuer Näherungswert:  1.4142135623746899
Schritt  5
Relative Änderung:  1.1276535261092282e-12
Neuer Näherungswert:  1.4142135623730951
Das Ergebnis ist  1.4142135623730951
Check:  1.4142135623730951

In [ ]:

Andreas Krassnigg: Physics, AI and Data Science

AI expert and lecturer at the University of Graz

Einführung und einfache Algorithmen

1 Einführung und einfache Algorithmen¶

1.1 Einfaches Beispiel: Addieren aller natürlichen Zahlen bis zu einer bestimmten Zahl N¶

1.2 Einfaches Beispiel: Berechnen der ersten N Primzahlen ¶

1.3 Zeit-Komplexität¶

1.4 Übungsaufgabe: Implementieren Sie eine einfache Version des Newton-Raphson Verfahrens zum Finden einer Nullstelle einer Funktion¶

Leave a Reply Cancel reply

1 Einführung und einfache Algorithmen¶

1.1 Einfaches Beispiel: Addieren aller natürlichen Zahlen bis zu einer bestimmten Zahl N¶

1.2 Einfaches Beispiel: Berechnen der ersten N Primzahlen¶

1.3 Zeit-Komplexität¶

1.4 Übungsaufgabe: Implementieren Sie eine einfache Version des Newton-Raphson Verfahrens zum Finden einer Nullstelle einer Funktion¶

Leave a Reply Cancel reply

1.2 Einfaches Beispiel: Berechnen der ersten N Primzahlen ¶